In the current example, two representative volume elements are considered, the square and hexagonal arrays. However the self-consistent micromechanics method can be applied to other representative volume element geometries that meet the doubly periodic condition. A
schematic of each geometry is given in Figure 1. The first two columns in Table 1 are the input constituent material properties for an IM7/8552 carbon fiber, epoxy matrix composite. The final two columns in Table 1 give the predicted homogenized composite properties for the two representative volume elements.
|
Property |
Matrix |
Fiber |
Square Cell |
Hex Cell |
|
E1 (GPa) |
4.76 |
276.0 |
167.5 |
167.5 |
|
E2 (GPa) |
4.76 |
19.5 |
11.5 |
10.7 |
|
E3 (GPa) |
4.76 |
19.5 |
11.5 |
10.7 |
|
G12 (GPa) |
1.74 |
70.0 |
6.78 |
6.30 |
|
G13 (GPa) |
1.74 |
70.0 |
6.78 |
6.30 |
|
G23 (GPa) |
1.74 |
5.74 |
3.10 |
3.34 |
|
V12 |
0.37 |
0.28 |
0.31 |
0.31 |
|
V13 |
0.37 |
0.28 |
0.31 |
0.31 |
|
V23 |
0.37 |
0.70 |
0.57 |
0.60 |
|
a1 (10-6/°C) |
64.8 |
-0.4 |
0.41 |
0.41 |
|
a2 (10-6/°C) |
64.8 |
5.6 |
34.7 |
35.1 |
|
a3 (10-6/°C) |
64.8 |
5.6 |
34.7 |
35.1 |
|
Table 1. Fiber, matrix and equivalent homogenized medium material properties |
 |
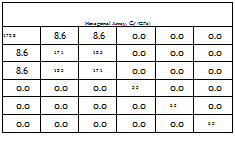 |
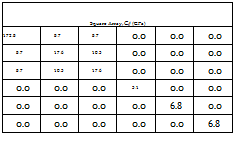
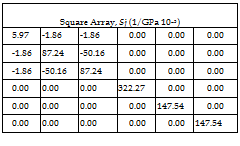
The homogenzied stiffness matrix (Cij) is first calculated from Equation 3. Equation 13 shows the calculations used to determine the homogenized engineering elastic constants from the homogenzied stiffness matrix. Shown in Tables 2 and 3 are the homogenized stiffness matrix and the homogenized compliance matrix (Sij), respectively. The predicted engineering constants are used as inputs in the laminate level analysis.
|
[S № I’ |
(13a) |
|
£1 = 1/ S11, £2 = V S22, £3 = 1/ S33 |
(13b) |
|
: – S32/S22 , V13 = – S31/S11 , V12 = – S21/S11 |
(13c) |
|
G23 = 1/S44, G13 = 1/ S55, G12 = 1/S66 |
(13d) |
Table 2. Homogenized stiffness matrix representative volume elements
 |
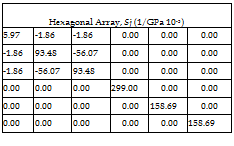 |
Table 3. Homogenized compliance matrix representative volume elements



