Compared with the previous achievements in this area, the works of Reeves [171] as well as Reeves and Blau [172] illustrate the different motivations underlying the modeling of plants.
 |
 |
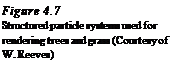![Подпись: One of the results of this specification is a quite primitive branching model, by which branches are produced recursively and then are attached to the trunk. Only the global form of the tree is given here. However, since the algorithm generates very regular branching - just like in all other procedures previously discussed - randomness is introduced later. If a generated branch is small enough, particles in the form of small colored balls are attached to it. The results are surprisingly realistic, in particular in the final result of the work, the film “The adventures of Andre and Wally B.”[124]. The main reason for this is certainly the perfect coloring of the models in combination with sophisticated shading models, which are also described in [172].](/img/1316/image119_3.gif "Generation Using Particle Systems") |
![Подпись: Fractal Tree Model Inspired by the discovery of fractals and the works of Mandelbrot [126, 127] during the mid-1980s, a number of computer-graphics scientists became in-volved with the aspect of fractal creation for the modeling of natural objects. These procedures are mostly recursive, since this has proven to be an easy way to simulate the self-similarity often found in trees. In a recursive procedure the heart of the computation is self-initiating, meaning it initiates itself automatically, over and over again. Oppenheimer’s algo-](/img/1316/image120_2.gif "Generation Using Particle Systems") |
Reeves, employed with Lucasfilm, needed a fast, relatively realistic method to represent vegetation such as forest or meadows. The botanical correctness of the models was in this case not of major importance; significant, however, was the overall realistic appearance. This is, as already pointed out in the introduction, with many computer-graphics applications a legitimate decision, since often a simulation has to be produced only once for a certain project.
Chapter 4 rithm [150] uses a method that recursively calls itself for the simulation of the
Procedural Modeling branching along a trunk, and to generate smaller branches along the large ones.
This can be continued arbitrarily, so that ever-finer branches develop. However, in practice, after a certain number of branches have been generated, the procedure is stopped.
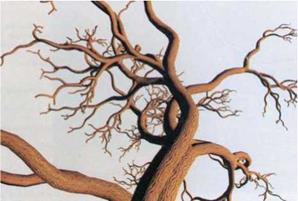Figure 4.8 Fractal tree model (Courtesy of P. Oppenheimer)
To oppenheimer it was particularly important to quickly produce a representation to easily facilitate the individual parameterization of the model. Contrary to Reeves and Blau’s branching structure, detail modeling must therefore be parameterized relatively finely. Here, also curved sections are used for the first time, to ensure a more realistic outlook of the trunk and its branches. one of the main assertions in oppenheimer’s article describes the relation of the geometry and topology of trees for the purpose of modelling in computer graphics: “… the key to realistic modeling, the diversity of trees, lies in controlling the geometric interpretation. Many different topologies were used in this project. But varying the geometric interpretation of a single topology, one could still generate a wide variety of trees each with its own distinct taxonomic identity.” Also here the focus is primarily on the visual representation, this time in particular on the detailed branching structure.
Contrary to Aono and Kunii [5], Oppenheimer uses a simple monopodial branching model with parameters for the branching angle, size ratio of father and child branches, degree of tapering along the trunk and the branches, number of branches per trunk segment, and the deviation angle.
In the following production process, similar to Reeves and Blau[3], the segments of the trunk and the branches are generated with a recursive algorithm. Within the transformation, the upper parameters ensure that natural forms develop. In pseudocode the form of the algorithm is written as follows:
Algorithm 4.1:
Procedure fractaltree() begin
draw actual branch segment
if small enough /* stop criterion */
then draw leaf else begin
transform actual branch
fractaltree() /* recursive call */
repeat n times
begin
transform for branching
fractaltree() /* recursive call */
end end
end
In order to interrupt the strict self-similarity of a recursively constructed tree, Oppenheimer uses random parameters, which he varies in each case depending on a function of a given average value and standard deviation. The trunk and the branches are modeled as a generalized cylinder using the connection of the individual segments. The realistic appearance of the bark is generated using a horizontally running saw tooth function. This generates a vertical striped pattern, which is modulated by adding a noise function in order to replicate the irregularities of the bark. The Brownian noise used here is treated more closely in Chap. 7, where it is used for the simulation of terrain, a further natural object with fractal characteristics.
Figure 4.8 illustrates the result of a recursive procedure. Oppenheimer asserted that he was able to render trees of such complexity in real time on an Evans and Sutherland graphics workstation.
