Geometrical and Topological Models

Already in the preceding chapters, we differentiated between the geometrical and topological characteristics of trees. At this point, we reiterate these differ­ences, for the sake of clarity. In the following chapters, when we speak about the production or rendering of a tree, we specifically mean the reproduction of the outer appearance of the plant, its morphology. In computer graphics, this reproduction is achieved through the plant geometry by means of many small surfaces in 3D space, usually in the form of triangles and squares. Thus, we speak of a geometrical tree when a botanical tree is reproduced visually by its shape. In other words, a geometrical model approximates the surface of its botanical counterpart.

In contrast, the topological tree takes into account only the number and types of branching, and indicates, how many branches develop from one branch and again how many secondary branches emerge from the first set. The form and appearance of the branches are not of interest here. Two geometrically very dif­ferent trees can, viewed topologically, have the same description. Just imagine that the points on the surface of an object are connected by rubber bands, the two structures are then topologically equivalent if we can transform the first geometry by bending and twisting it into the second. For example, this is not possible if we want to transfer the surface of a ball into a coffee cup, since the cup has a handle that cannot be achieved this way.

Almost all botanical trees are binary trees in this sense, with the exception of the leaf arrangement described in Sect. 2.1 which topologically represents a tertiary tree with a branching divided into three parts (see Fig. 3.1).

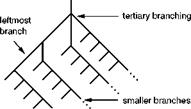
Topological trees can therefore be described using the following pattern: a tree is a quantity of knots, and of edges that connect the knots. There are two kinds of knots: internal knots (branching knots), and external or terminal knots, also called leaves. Each internal knot has two children; in a tertiary tree we find three. The external knots do not have children. An internal knot, seen from the point of view of its children, is called the father knot. Similar one can call the corresponding edge a father branch and an outgoing edge a child branch.