The geometry produced with the horn component is used as the basis for all types of stems, branches or trunks, and it can additionally be used for the rendering of other organic objects (see [150, 219]). Occasionally, it is termed a generalized cylinder and is developed from the triangulation of tube primitives, as shown in Fig. 6.2. Aside from tubes also other primitives can be used and arranged along a curve using the same mechanism.
The horn component additionally permits us to multiply the geometry of successive components. In this case, the local coordinate systems of the child components are attached to the spots along the curve, which together with the tube primitives define the cylinder. Hence, the horn component produces geometry, and at the same time functions as a multiplying component. The same holds true for the tree component in the following section.
Tree Component
just like the horn component, the tree component also produces a generalized cylinder.[5] [6] The difference to the horn component is simply the way successive components are multiplied and over which parameters the form of the cylinder can be affected.
Usually a tree is constructed as a cascade of tree components or is defined over a recursion. In the latter case, however, the parameters cannot be set individually for each branching level, which often is a disadvantage.
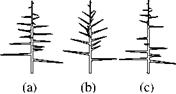
The parameters of the tree component are divided into three groups. One group determines the positioning of the branches. Here the branching angle (see Fig. 6.4b) as well as the branching characteristic can be adjusted. The branching characteristic defines how many branches per unit length along the trunk are produced (Fig. 6.4c). The adjustment is handled by the user via a density curve. Also the deviation angle between neighboring branches can be modified. By default, here the Fibonacci Angle, i. e., the Golden Section cut, is applied (see Sect. 3.4).
|
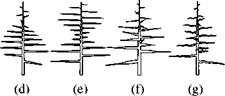
Further parameters determine the size of the branches (Fig. 6.4e), their thickness along the branch axis (f), the gnarliness (g) as well as the directional change of the trunk at a branching. Additionally, the form of the trunk can also be defined directly over a spline function.
Similar to the leaves, phototropism and gravitropism can also act on the generalized cylinders of the trunk and the branches. For this reason, the produced tube primitives are turned locally towards the light field, which altogether produces a bending of the geometry. In addition, the appearance of many trees is significantly determined by these parameters, though the effect can also be used to model deformations caused by wind influences.
In tree modeling another crucial difference between classic rule-based systems and rule-based object production comes to light. While with rule-based systems the appearance of a plant is controlled via the modification of local parameters, here global aspects are modeled. An example is the size of the forking branches, which is indicated by a function over the length of the trunk. Modeling with L-systems is at this point rather difficult, since the smallest local changes over several recursion stages can cause great differences in the appearance. As already mentioned, this problem is lessened through the use of editable functions, as demonstrated in Sect. 5.10.
