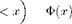The modeling of synthetic landscapes not only presupposes a natural look of the plant cover, but also requires the terrain itself to appear as a faithful replica of a scene in nature. Since there exists a complex interplay between the vegetation and the local peculiarities of a landscape, suitable specification methods for terrain, as well as other abiotic environmental factors, must be found. Of course, these should work as automatically as possible, since, especially for large terrains, it would be too cumbersome to implement interactions manually. In this chapter we introduce some of these methods, again with a special focus on computer graphics and related fields.
For creating a terrain, it is useful to resort to fractal methods, already referred to in Sect. 3.3. There we already pointed out that the visual attributes of coastlines and mountain ranges prompted the search for new mathematical descriptions. One of the first-observed natural processes with fractal attributes was the movement of small particles in an oil emulsion, the so-called Brownian motion [127, 158].
The microscopic movement of a particle is caused by the thermal motion of the molecules that hit the small particle randomly from different directions. The developing path has a fractal character insofar as it exhibits self-affinity within a large scaling range, and thus, is self-similar except for a scaling factor. The fractal character of the Brownian motion is here significant, since it offers a very elegant option for creating a natural-appearing terrain in a simple way. Here, the Brownian motion is understood as a function, and the function values are interpreted as elevation values. In the following, this is demonstrated with a one-dimensional function, and is then extended to two-dimensional fields. The developing data later serve as input data for a system for the specification of vegetation.
To store the data of a terrain, a height map is used. In a height map, for each place on the surface exactly one elevation value is denoted; the height can be interpreted as a function over the surface. This description has a slight disadvantage in that it does not permit the rendering of caves or overhangs, although, this is not a significant constraint when modeling landscapes. The advantages,
|
■ It is a nondifferentiable function of time with a characteristic frequency spectrum1 1/fe, where the frequency is denoted by f and в є [1,3] is the scaling factor. ■ It is statistically self-affine: Its appearance is self-similar in all scalings with the application of an additional vertical scaling factor, meaning we achieve a similar look if we scale the function and then add a vertical scaling factor. There are three possibilities for generating a Brownian motion via a computer. The first option is the use of a sum of sine functions with random phase and an amplitude that is determined over the 1/fe-criterion. This procedure is similar to the process of the Fourier transform: The function is synthesized by a sum 1 The frequency spectrum of a function is obtained, in that the function is described as a sum of trigonometric functions with individual amplitudes. These amplitudes can then be denoted as function of the frequency, this is termed the frequency spectrum. The transformation between the function and the frequency spectrum is called the Fourier transform. |
|
|
 |
|
 |
|
|
|
|
|
|