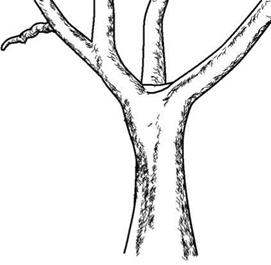
cross-hatchings usually serve the rendering of lighting effects in illustrations. They are applied to those regions that lie in the shadow, and in contrast to adding details they permit an additional blackening that has a more two-dimensional effect. Hence, they are rather used for smooth surfaces such as the trunks and branches (compare Fig. 11.8). However, in the lower part of Fig. 11.6, cross-hatching can also be seen in the foliage.
Methods for the automatic rendering of cross-hatching again must include algorithmic approaches. At the beginning of the chapter, we addressed the method of Salisbury, Winkenbach and Salesin, who solved this problem with special stroke textures that display cross-hatching. Through the arrangement and blending techniques, cross-hatching can be rendered that consists of many short strokes. Producing longer strokes, however, often proves a failure.
Winkenbach and Salesin [233] extend the approach to parametric surfaces. Section 11.4
Elber also presents an algorithm for the cross-hatching of parametric surfaces Rendering of Cross-Hatching
[55, 57]. In both cases the authors have illustrated cross-hatching with longer
strokes. However, both approaches have the disadvantage of being dependent
 |
on a parameterization of the geometry which is often poor or not even present.
The parameterization allocates to each vertex two additional numbers in an interval [0… 1], which aim at pointing to a position of the texture. The place described by this vector is to be colored with the respective pixel of the textures. The parameterization is either to be given for each point of the surface beforehand or is specified at least for the corners of the surface and is then determined by interpolation.
In the case of tree models, parameterization unfortunately often is not given. Hence, surfaces of a tree skeleton, and also many other models in computer
graphics, consist of triangular sets without explicit parameterization. Consequently, methods that do not need parameterization should be preferred.
Such a method is the algorithm of Saito and Takahashi from Sect. 11.1. Aside from the contour lines, in the work the production of simple cross-hatchings using depth values of pixels is discussed. The procedure is demonstrated in simple examples. The results here are individual pixel values, whose grayscale values are changed. Leister presents in [114] another parameter-independent method for cross-hatching of surfaces. He uses a special variant of the raytracing algorithm in combination with image processing. The objects are here attributed with a special volume texture, consisting of black and white regions. The resulting image displays the intersection of the black and white texture function with the geometry on the surface that has a cross-hatched appearance. An advantage of the method is the inclusion of highlights, reflection, and shadows into the cross-hatching process, which is only possible with the implementation of raytracers or other global light simulation algorithms. Disadvantages are the artifacts and the aliasing effects in the images as well as the difficulty of adjusting the cross-hatching directions to the geometry.
|
(a)
halftoning ^ Both disadvantages are avoided using the method of Ostromoukhov [151] in which the rendering of cross-hatching is done without any three-dimensional model information, and is executed interactively. A grayscale image serves as the input for the object to be drawn. The user defines the line directions for those areas to be cross-hatched, by deforming a standard pattern consisting of parallel lines. This takes place through a geometric transformation or a so – called morphing algorithm. Both allow an almost arbitrary deformation of the standard pattern. The image is subsequently rendered, in that the directions of the cross-hatching lines are generated, and their thicknesses and densities are varied so that the grayscale values of the input images are approximated.
This method is a half-toning procedure (see again [221]) that translates the grayscale values of a given image into another image consisting solely of black and white pixels. Similar methods were implemented in Chap. 8 to specify plant positions. Ostromoukhov introduced in recent years several artistic halftoning procedures, in which, aside from the visual optimal grayscale value approximation, increasingly artistic freedom can be integrated [152, 153, 154]. Additional works on this subject were authored by Buchanan [24] as well as by Verevka and Buchanan [223, 224]. Also here artistic effects are integrated into the half-toning process in order to give the images the appearance of a drawing.
