Application of uniform temperature change, AT

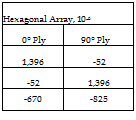
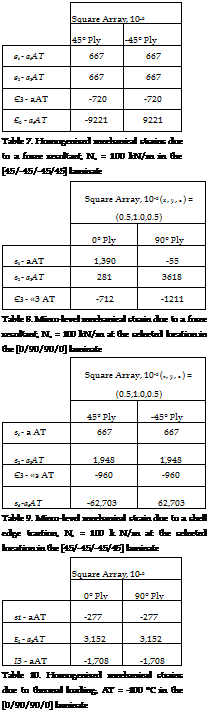
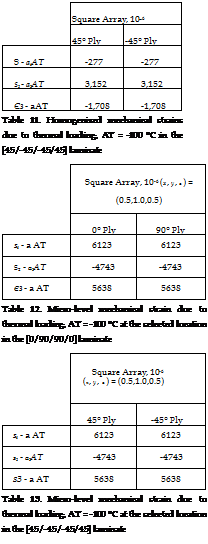
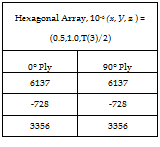
Next, consider the cross-ply and angle-ply laminates subjected to a uniform temperature change of AT = -100 °C. The macroscopic strain state in each lamina is determined using the classical laminate theory analysis outlined in Section 5.3 with a lamina thickness, t, of 0.2 millimetres. The homogenized mechanical strains in the cross-ply and angle-ply laminates are given in Tables 10 and 11 respectively. The strain within both representative volume element is found from the homogenized states of strain by applying the influence matrices and thermal superposition vectors according to Equation 8. Mechanical strains are present at the lamina level and at the micro-level for the thermal loading case. This is due to a mismatch in the homogenized coefficients of thermal expansion of the lamina and a mismatch in the coefficients of thermal expansion of the constituents. Again, the influence matrices shown in Table 4 and the thermal superposition vectors of Table 5 are used to determine the strain in the matrix phase at the location (x, y, z) = (Lx/2, Ly, Lz/2) for both representative volume elements. Tables 12 and 13 list the strain state at the selected location within the matrix for the cross-ply and angle-ply laminates, respectively. It is obvious that identical results are obtained for the [0/90/90/0] and [45/-45/-45/45] laminates because the two laminates thermally identical after a rotation of 45°. As such, both laminates have identical states of strain in the material principal coordinates.

	Hexagonal Array, 10-6 45° Ply -45° Ply 672 672 672 672 -748 -748 -9921 9921
Hexagonal Array, 10-6 (x, У, z ) = (0.5,1.0,T(3)/2) 0° Ply 90° Ply 1,396 -52 491 3,630 -655 -1,183
Hexagonal Array, 10-6 (x, y, z ) = (0.5,1.0,T(3)/2) 45° Ply -45° Ply 672 672 2060 2060 -919 -919 -46,629 46,629
Hexagonal Array, 10-6 0° Ply 90° Ply -263 -263 3,206 3,206 -1,823 -1,823

6.

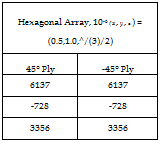Conclusions

A computationally efficient method for estimating the microscopic strain field within the discrete phases of a heterogeneous medium consisting of collimated, continuous fibers within an isotropic matrix has been developed. The goal of the development has been to provide an essential link in a multi-scale analysis of a composite structure. The structural loading and deformations at the macro-scale can be related to the state of strain within the fiber and matrix phases at the micro scale by using the self-consistent micromechanics method. The model utilizes a conventional influence function formulation and considers thermo-mechanical deformations. Results have been presented that illustrate the utility of the approach in determining microscopic state of strain in the [0/90/90/0] and [45/-45/-
45/45] laminates. Enhanced strain components within each of the lamina were calculated for both uniaxial loading and a uniform change in temperature.

The present example showed results extracted for a single point within the representative volume element. As shown in Figure 3, the influence matrix and thermal superposition vector are field values. Therefore, the state of strain within the representative volume element can also be represented as a field value. As such, the analysis is not limited to analysis of the state of strain at a single point. However, the reader may choose as many interrogation points as are required in order to address de-homogenization of all of the phases or to meet a specific need with a minimum computational cost.

Microstructures found in fiber reinforced composites typically consist of an irregular array of fibers which differ from the representative volume elements analysed herein. An efficient method for dealing with variability is through the use of a statistically equivalent periodic unit cell. With this approach, a computational step is used to generate an equivalent representative volume element that replaces the actual complex geometry. This method has been applied at several length scales including a unidirectional fiber tow (Zeman and Sejnoha, 2007).

The main assumption implicit in the analysis is that the representative volume element is subjected to a uniform state of strain. Certainly, this is not true at all locations within a laminate. Examples include areas with large strain gradients or locations with discontinuities in the assumed periodicity such as ply interfaces. In light of these limitations, the described method provides a reasonable first order approximation of the state of strain within the constitutive phases of an ordered heterogeneous medium.