Covalent materials such as II-IV semiconductor compounds ZnX (X=S, Se, Te) have been extensively studied for their intrinsic structural, optical, and elastic properties such as energy gap, charge density, lattice constants and bulk modulus. However, bulk modulus has been found to correlate well with strength and hardness in many materials and those with largest bulk moduli are usually expected to be the hardest materials. Therefore, one of the important parameters that characterize the physical property of a material system is the material stiffness and its corresponding bulk modulus which measures the degree of stiffness or the energy required to produce a given volume deformation. The bulk modulus reflects important bonding characters in the material and, for many applications, is used as an indicator for material strength and hardness. Early experimental and theoretical investigations for bulk modulus were reported in (Cohen, 1985; Lam et al., 1987). Cohen (Cohen, 1985) obtained an empirical expression for the bulk modulus based on the nearest-neighbour distance. His theoretical and experimental results were in agreement. Lam et al. (Lam, 1987) obtained an expression for bulk modulus using the total energy method with acceptable results. The bulk modulus for the semiconductor compounds was found to be inverse proportionally correlated to the lattice constants (Lam et al., 1987; Al-Douri et al., 2004).
Physical properties are intrinsic characteristics of matter that are not affected by any change of the coordinate system. Therefore, tensors are necessary to define the intrinsic properties of the medium that relate an intensive quantity (i. e. an externally applied stimulus) to an extensive thermodynamically conjugated one (i. e. the response of the medium). Such intrinsic properties are the dielectric susceptibility, piezoelectric, and the elasticity tensors. An interesting feature of the decompositions is that it simply and fully takes into account the symmetry properties when relating macroscopic effects to microscopic phenomena. One can directly show the influence of the crystal structure on physical properties, for instance, when discussing macroscopic properties in terms of the sum of the contributions from microscopic building units (chemical bond, coordination polyhedron, etc). A significant advantage of such decompositions is to give a direct display of the bearings of the crystal structure on the physical property.
The proposed procedure in this chapter has introduced a method to measure the stiffness and piezoelectricity in fiber reinforced composite and piezoelectric materials using the norm criterion on the crystal scale. In this method, norm ratios proposed to measure the degree of anisotropy in an anisotropic material, and compare it with other materials of different symmetries. It was able to segregate the anisotropic material property into two parts: isotropic and anisotropic parts. Of the new insights provided by invariance considerations, the most important is providing a complete comparison of the magnitude of a given property in different crystals. Such a comparison could be obvious for average refractive index, even birefringence, piezoelectricity, electro-optic effects, elasticity, etc. From a device point of view, the new insights facilitate the comparison of materials; one is interested in maximizing the fig. of merit by choosing the optimum configuration (crystal cut, wave propagation direction and polarization, etc); and one wants to be able to state that a particular material is better than another for making a transducer or modulator (Jerphagnon, 1978). It is most suitable for a complete quantitative comparison of the strength or the magnitude of any property in different materials belonging to the same crystal class, or different phases of the same material. The norm concept is very effective for selecting suitable materials for electro-optic devices, transducers, modulators, acousto-optic devices. Therefore, using the elastic constant for anisotropic material, an elastic stiffness scale for such anisotropic material, and a scale to measure the isotropic elasticity within the material will be discussed. Besides, the microscopic origin of the overall elastic stiffness and bulk modulus calculation will be correlated with the structural properties parameter, i. e. lattice constant a, which represents some fundamental length scale for the chemical bond of the unit cell.
The elastic stiffness matrix representation for the isotropic system can be decomposed in a contracted form as:
|
:+C12 |
C 12 |
C 12 |
0 |
0 |
0 |
|
12 |
2C44+C12 |
C 12 |
0 |
0 |
0 |
|
12 |
C12 |
2C + C 44 C12 |
0 |
0 |
0 |
|
0 |
0 |
0 |
C 44 |
0 |
0 |
|
0 |
0 |
0 |
0 |
C44 |
0 |
|
0 |
0 |
0 |
0 |
0 |
C44 |
|
"1 |
1 |
1 |
0 |
0 |
0" |
" 4 |
-2 |
-2 |
0 |
0 |
0 |
||
|
1 |
1 |
1 |
0 |
0 |
0 |
-2 |
4 |
-2 |
0 |
0 |
0 |
||
|
1 |
1 |
1 |
0 |
0 |
0 |
-2 |
-2 |
4 |
0 |
0 |
0 |
||
|
A |
+A„ |
||||||||||||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
3 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
where
A1 3(C11+2C12)’ C11 2C44 + C12
(26)
A2 = 15(C11-C12 + 3C44)
where A1 and A 2 are the Voigt average polycrystalline bulk B and shear G modulus,
respectively. The decomposed parts of Eq. (25) designated as bulk and shear modulus are identical to those found in literature (Voigt, 1889; Hearmon, 1961; Pantea et al., 2009).
For cubic crystals such as the II-VI semiconductor compounds, there are only three independent elastic stiffness coefficients C11, C12, and C44 that can describe the mechanical elastic stiffness for these materials. The elastic coefficient C11 is the measure of resistance to deformation by a stress applied on the (100) plane, while C44, represents the measure of resistance to deformation with respect to a shearing stress applied across the (100) plane. These elastic coefficients are function of elastic material parameters, namely, Young’s modulus, shear modulus, and Poisson’s ratio. Thus, using the orthonormal decomposition procedure (Gaith & Akgox, 2005), the elastic stiffness matrix representation for cubic system can be decomposed in a contracted form as:
 |
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
![]()
where
A1-^3(C11 + 2C12) A2=15(Cn-C12 + 3C44> A3=T0(C12-Cn+2C44)
It can be shown that the sum of the three orthonormal parts on the right hand side of Eq.
(26) is apparently the main matrix of cubic system (Hearmon, 1961). Also, the first two terms on the right hand side are identical to the corresponding two terms obtained in Eq. (23) for the isotropic system (Hearmon, 1961). Hence, it can be stated that the cubic system is discriminated into the sum of two parts: isotropic part (first two terms), and anisotropic part (third term). The latter term resembles the contribution of the anisotropy on elastic stiffness in the cubic system. On the other hand, the first term on the right hand side of Eqs (23) and (27), designated as the bulk modulus, is identical to Voigt bulk modulus (Hearmon, 1961).
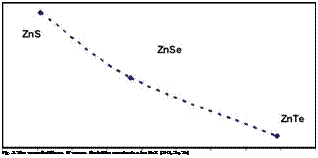
Nowadays, the necessity of alternative energy use is widely accepted. In solar energy technology, thin film solar technology based on the II-IV semiconductor compounds, is very promising due to lower production costs and shorter energy pay back times (Fischer, 2006). For these compounds, a successful interface between absorber and buffer layers with alternative and promising non-toxic materials requires compositional and electronic material characterization as a prerequisite for understanding and intentionally generating interfaces in photovoltaic devices (Fischer, 2006). On the other hand, stability of ZnTe/ZnS solar cells is of concern for their application in space, where the cells have to withstand high energy particles, mainly electrons and protons that can cause severe damage in solar cells up to a complete failure. Therefore, the radiation hardness and damage mechanism of the ZnTe solar cells is associated with the overall elastic stiffness and bulk modulus (Batzner, 2004). Table 5 presents the materials elastic stiffness coefficients, calculated bulk B and overall elastic stiffness N moduli for the II-VI semiconductor ZnX (X=S, Se, and Te) compounds. Fig. 1 shows clearly the correlation between overall elastic stiffness N and bulk modulus B. Quantitatively, the overall elastic stiffness increases as the calculated bulk modulus B increases. Besides, the calculated bulk moduli are identical to those found by theory of anisotropy (Hearmon, 1961), and are in agreement with experimental values (Cohen, 1985) with maximum error of 8.5 % for ZnTe. The calculated bulk moduli obey the cubic stability conditions, meaning that C12 < B < Сц. Fig. 2 shows that the bulk modulus is inversely proportional to lattice
constants a which was confirmed in several studies (Lam et al., 1987; Al-Douri et al., 2004). Consequently, from Fig. 3 the overall elastic stiffness N is inversely proportional to lattice constants a, as well. Fig. 1-3 indicate that among the three compounds under examination, ZnS has the largest elastic stiffness, largest bulk modulus (lowest compressibility), and lowest lattice constant, while ZnTe, in contrary, has the smallest elastic stiffness, smallest bulk modulus, and largest lattice constant. Therefore, the overall elastic stiffness and bulk modulus, the only elastic moduli possessed by all states of matter, reveal much about interatomic bonding strength. The bulk modulus also is the most often cited elastic constant to compare interatomic bonding strength among various materials (Pantea, 2009), and thereafter the overall elastic stiffness can be cited as well.
For the isotropic symmetry material, the elastic stiffness tensor is decomposed into two parts as shown in Eq. (23), meanwhile, the decomposition of the cubic symmetry material, from Eq. (27), is consisted of the same two isotropic decomposed parts and a third part. It can be verified the validity of this trend for higher anisotropy, i. e., any anisotropic
|
C11 |
C12, |
C44 |
N |
B |
Bexp (Cohen, 1985) |
a (Chelikowsky, 1987) |
|
|
ZnS |
104 |
65 |
46.2 |
266.5 |
78 |
77 |
0.54 |
|
ZnSe |
95.9 |
53.6 |
48.9 |
244.0 |
67.7 |
64.7 |
0.57 |
|
ZnTe |
82 |
42 |
55 |
224.0 |
55.3 |
51 |
0.61 |
|
Table 5. Elastic coefficients (GPa) (Cohen, 1985), overall stiffness N (GPa), bulk modulus B (GPa), and lattice constants a (nm) |
270
 260
260
250 Q.
CD
240 230 220
0. 53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61 0.62
a (nm )
|
Niso |
Naniso |
N |
N iso N |
N anis N |
B |
A |
|
|
ZnS |
262 |
49 |
266.5 |
0.9830 |
0.1836 |
78 |
0.54 |
|
ZnSe |
238.7 |
50.9 |
244.0 |
0.9780 |
0.2084 |
67.7 |
0.57 |
|
ZnTe |
214.6 |
64.2 |
224.0 |
0.9581 |
0.2865 |
55.3 |
0.61 |
|
Table 6. The overall elastic stiffness N (GPa) and norm ratios for the II-IV semiconductor compounds ZnS, ZnSe, and ZnTe |
The norms and norm ratios for ZnS, ZnSe, and ZnTe are calculated and presented in Table 6.
Niso
From the table, interesting phenomena are observed; as the isotropic ratio —3^° increases, Nanis
the anisotropic ratio —decreases, which confirms the definitions of these two ratios, and the bulk modulus increases at the same time. Therefore, the nearest material to isotropy
Niso
(or least anisotropy) is ZnS, with —Tso = 0.9830, in which corresponds to the largest bulk
Niso
modulus B = 78 GPa. The least isotropic (or nearest to anisotropy) is ZnTe, with —=
0.9581, in which corresponds to the smallest bulk modulus B = 55.3 GPa. Since the cubic system is the nearest to isotropy among the anisotropic systems, the calculated values of
Niso
the material is. A reverse trend correlating the norm ratios and lattice constants can be seen from the table; the closer the material is to isotropy, the smaller the lattice constant for the material is.
The overall elastic stiffness of II-IV semiconductor compounds ZnS, ZnSe, and ZnTe is calculated and found to be directly proportional to bulk modulus and inversely proportional to lattice constants. Among these compounds, ZnS has the largest overall elastic stiffness and bulk modulus and the smallest lattice constant. Meanwhile, ZnTe has the smallest overall elastic stiffness and bulk modulus and the largest lattice constant. The Norm Ratio Criteria (NRC) is introduced to scale and measure the isotropy in the cubic system material among the semiconductor compounds ZnS, ZnSe, and ZnTe. Hence, a scale quantitative comparison of the contribution of the anisotropy to the elastic stiffness and to measure the degree of anisotropy in an anisotropic material is proposed. ZnS is the nearest to isotropy (or least anisotropic) while ZnTe is the least isotropic (or nearest to anisotropic) among these compounds. These conclusions can be investigated on the II-IV semiconductor compounds CdX (X=S, Se, Te) in similar manner.


