In the mathematical description of any phenomenon or process, we solve two conflicting objectives. On the one hand it is necessary to obtain a simple model with a small number of parameters and we have research equipment for determine it. On the other hand the model should be adequate to the real process with acceptable accuracy. Use for this purpose of simple linear mathematical models without taking into account the many phenomena of the process, such as, for example, outflow the resin under the pressure, dependence of thermophysical properties on temperature, degree of cure and the filling factor leads to large modeling errors and uncertainty of the solutions.
Technologies for obtaining large-size thick-walled products have the greatest interest. Examples of such technologies include the hot pressing in mold, autoclave vacuum forming and winding on the mandrel (Balakirev et al., 1990). Products that produced by these technologies tend to have a flat shape or a small curvature, which allows to consider such products as the unlimited plate and to use one-dimensional mathematical model of the process, although there are no obstacles to the use of more complex models. A mathematical model for each technology has its own characteristics, but at the same time, a unified framework (Dmitriev & Shapovalov, 2001). Typically, a mathematical model of a hot curing of composites when regulating the temperature of the forming tooling U(t) is a system of differential equations of heat and mass transfer, kinetics of curing, leaking (extrusion) of resin, compacting the material in the process of forming and rheological equations of state. As an example, the method of calculating the optimum curing cycles of composites for the thick-walled products or panels, produced by autoclave vacuum molding is considered.
For the autoclave vacuum molding the dominant processes in the material are heat-mass transfer and curing. A mathematical model of the autoclave molding and curing of products made of thermosetting composites in multi-layer i = 1,…5 technology package, taking into account the outflow of resin is a system of differential equations of the following:
– heat-mass transfer:
T = T(x, t), Li-1 < x < Li, L0 = 0, 0 < t < tf, i = 1,…5,
C, = Ci(T), . = .(T), Wx,= 0, Qfi = 0, Li = const, at i = 1, 4, 5,
C2 = C2(T, P2,Y2), .2 = .2(T, P2,Y2), Wx2 * 0, Qf2 * 0, Ll < x < L2(t), i = 2,
C3 = Cs(T, P3,Y3), .3 = .3(T, P3,Y3), W3 * 0, Qp * 0, L2(t)<x<lbi(t), i = 3,
C3 = C3(T), .3 = Ae(T), Wx3 = 0, Qf3 = 0, lbi(t) < x < L3, i = 3,
![]()
|
|
||
|
|||
|
|||
|
|||
|
|||
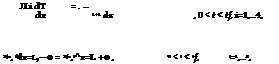 |
– kinetics of cure
spL k(P)exp[-E(P)/ RT], p< 1,
dt[ 0, P = 1,
![]()
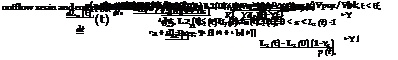 |
|
Pi = Pi(x, t), Li-1 < x < Li, 0 < t < tf,
P,(x,0) = P0i(x) > 0, i=2, 3,
Ppr (0) Mre (0) Ppr. min Mr
PreMpr (0) , ^ PreMpr,
where C – volumetric heat capacity, J/(m3’K); E – activation energy of curing, J/mol; E, – activation energy of viscous flow, J/mol; f – initial distribution of temperature, K; Qf – full heat of the reaction, J/m3; k – permeability, m2; L – thickness of the product, m; £ bl – the depth of penetration of the resin in the bleeder, m; £ fi – the thickness of the tightly compressed layers of filler, m; M – mass, kg; n – number of layers of prepreg in the product; – Po, Pa – the pressure in the autoclave and vacuum bag, Pa.; R – universal gas constant, J/(mol’K); T – temperature, K; Ta – the temperature of heating air, K; t – time, s; x – spatial coordinate, m; V – volume, m3; w – speed of the current resin, m/s; a – heat-removing factor, W (m2,K); в – the degree of curing; у – the mass contents of the resin in the prepreg; ф – kinetic function, 1/s; X – thermal conductivity, W/(m-K); , – dynamic viscosity of the resin, Pa’s; p – density, kg/m3; ^ – porosity bleeder;
indexes: re – resin; fl – fabric filler; bl – bleeder; pr – prepreg; s – start; f – final; a – the air. Moreover, x = 0 corresponds to the lower surface of the metal tool plate, x = L5 – corresponds to the upper surface of the airweave breather layer; i=1, 2,…5 – correspond to each layer of a technological package: i = 1 – metal tool plate, i = 2 – laminate prepreg, i = 3 – bleeder, i = 4 – perforated metal sheet, i = 5 – airweave breather layer.
In autoclave vacuum molding the temperature of heating air Ta(t) or the temperature of the forming tooling T(L1,t) are control parameters U(t).
The proposed model describes only the changes in the size of the composite products, which are caused by changes in the content of the resin. Shrinkage caused by changes of molecular structure of the resin during curing is not considered.
|
№ |
Model parameters |
Designation |
|
Determined experimentally in the CMS |
||
|
1 |
Volumetric heat capacity |
C(T, e,Y) |
|
2 |
Thermal conductivity |
X(T, e,Y) |
|
3 |
Full heat of the reaction |
Qf |
|
4 |
Activation energy of curing |
E(P) |
|
5 |
Kinetic function of curing |
Ф( в) |
|
6 |
Activation energy of viscous flow |
E, |
|
7 |
Dynamic viscosity of the resin during cure |
~(P) |
|
8 |
Permeability of filler |
kfi |
|
9 |
Permeability of bleeder |
kbi |
|
Determine additional |
||
|
10 |
Porosity of bleeder |
|
|
11 |
Thickness of the tightly compressed layers of filler |
Lpr. min |
|
12 |
Initial thickness of the product |
Lo |
|
13 |
Initial prepreg degree of curing |
в о |
|
14 |
Initial mass contents of the resin in the prepreg |
Ys |
|
Table 1. Determined experimentally parameters of the mathematical model |
The forming often occurs without the outflow of resin from the prepreg in the technological package or in a closed mold by direct hot pressing. Then the mathematical model is simplified to two differential equations, this equation of heat conduction and kinetics. Accordingly, the number needed to identify the characteristics of the material decreases.
One of key parameters of the mathematical model of curing process are the characteristics of a material, both in the cured a state and in the uncured state, and also during curing. They are not constant, but are a function of temperature T, the degree of curing p, resin content у or time t, which are subject to identification by experimental data (see table 1).
Typically, these parameters are determined from experiments using special techniques and devices. For their definitions are used: differential scanning calorimeter (DSC) for studying the thermal processes occurring in the prepreg on heating, thermomechanical analyzer (TMA), dynamic mechanical analyzer (DMA), thermal conductivity meters, etc.
However, currently available experimental devices and apparatus are intended primarily to study the properties of solid materials or cured composites or curing kinetics of the small size of samples in the absence of process pressure. Devices for the determination of rheological characteristics of thermosetting resins, typically built on traditional classical rheology and can measure the characteristics of the pure resin without the structural features of composite and production process (Kulichikhin & Astakhov, 1991). This restricts the use of standard methods and devices for studying the curing of composites, because they do not fully possible to determine all the parameters of a mathematical model of the curing process with all the relationships and features. Thus, to solve this problem it is necessary to use special methods and measuring devices that allow to determine the characteristics of composites in conditions close to conditions for the production of composites in the process. This path will allow more finely into account all the circumstances connected with the study of properties of composites and to obtain more precise parameters of the mathematical model.
Characteristics that are determined in conditions close to technological process are in some sense effective, that correspond to the peculiarities of the process and bear in itself factors and effects that not considered at the mathematical description and simulation. So promising are the methods and experimental devices that allow to study materials for the real designs using special samples and reproduce in the study of process conditions, that are process pressure, heating rate, peculiarities laying prepreg, study filled composite to replace the study of pure resin, etc. These requirements relate to the presence of interphase interactions occurring at the interface of resin-filler and influencing the kinetics of curing, as well as the influence of process pressure and laying on the thermal conductivity of the composite. An important condition for developing such devices, along with the ability to simulate technological modes of cure, is the ability to create special boundary conditions are necessary to simplify the algorithms for processing the experimental data and the desired accuracy of determine parameters.
Given the fact that the process of curing and polymer composites are highly informationintensive objects, their properties are often complicated functions, to solve the problem of determining the parameters of the mathematical model is necessary to use automation and computer equipment.
To determine the material characteristics and other parameters of the mathematical model we have developed a number of methods and the computer-measuring system (CMS) research of the curing of composites (Dmitriev et al., 2010). CMS allows to explore in the process of curing all the characteristics needed to solve the equations of the mathematical model of curing composites (1)-(10): thermophysical characteristics of composites C(T, p,y), MT, p,y) depending on the temperature T, the degree of curing p and resin content y, the rate of evolved heat of cure reaction W(t), full heat of the reaction Qf, kinetic characteristics, that are activation energy of curing £(P), the kinetic function ф(Р), which includes the speed and order of chemical reactions, rheological characteristics, that are activation energy of viscous flow £ц and effective viscosity of resin Д(Р) in the curing. Permeability fiber filler k is determined by CMS in conjunction with the effective viscosity as a complex p(P)/k and does not require additional study, but if necessary it can be determined with the help of special equipment. Other parameters of the material and products, such as the density p, the thickness of the product L, mass M, the number of layers of prepreg in the product n is determined by standard methods or set.
The research composites by CMS produced in the measuring cell in the range of temperatures from room to 270 °С.
The object of the experimental study is a specially prepared sample, which is a package thickness of 5…20 mm, assembled from several sections of the researched prepregs cut to a square with side 100 mm. Stacking layers of prepregs and orientation fiber of the sample performed similarly to industrial products: unidirectional, cross or cross-bias, etc. Samples of materials prepared on these conditions and their size allows to take into account in studied effective characteristics the rheological processes taking place during curing, the especial of stacking layers of prepreg in the product, to average a local inhomogeneity of the structure of materials and factor content of resin, which does not allow to perform other standard methods and devices, including scanning calorimetry method.
By means CMS in the measuring cell is organized the process of heating the studied sample, described by the (1) – (10), and measured over time following values: the time t, voltage of the heater u(t), the temperature in the 2…5 points on the thickness of the sample T(x, t), the thickness sample L(t), the force pressing the sample F(t), dielectric permittivity e(t) and dielectric losses tanS(t).
Research carried out for each sample in two phases: heating to cure and re-heating after cooling. During the first phase studied the kinetics of the cure, the flux of resin and the effective thermophysical characteristics of Cw(t(T)), £w(t(T)), including the rate of evolved heat of cure reaction W(t). In the second phase studied the properties of cured material Ccd(t(T)), £cd(t(T)). On the basis of these data are calculated C(T, p,y) and £(T, p,y). To research the kinetic and rheological characteristics conducted experiments on the cure at least for two samples with different rates of heating. The conditions of the experiment, ie voltage of core heater u, which determines the heating rate and the force F on the sample, are chosen to reproduce the technology modes and to ensure the minimum error of the desired characteristics. Dielectric characteristics of e(t) and tanS(t) are needed to determine the moment of pressure application and the completion of curing.
In the experiment CMS performs the primary processing of data and recording it to the hard disk, as well as testing and monitoring of the system. At the end of the experiment is performed calculations researched characteristics.
As a method of determining the thermophysical characteristics of C(T, p,y), £(T, p,y) used the method of integral characteristics (Dmitriev et al., 2010). Kinetic characteristics of £(P) and ф(Р) that are part of the equation of kinetics are determined by the rate of evolved heat of cure reaction W(t), measured in the curing of two or more samples heated at different temperature-time modes Tav(t). By measuring the thickness L(t) of curing sample at squeezing-out of resin are determined the rheological characteristics £ц and p(P) .
Calculated formulas and algorithms for processing of the experimental data obtained on the basis of established methods are the core software of CMS. Researched characteristics of composites and other parameters of the mathematical model are entered into a database of CMS and are the information basis for the automated calculation of the optimal curing cycles of the composite products for any thickness and configuration.
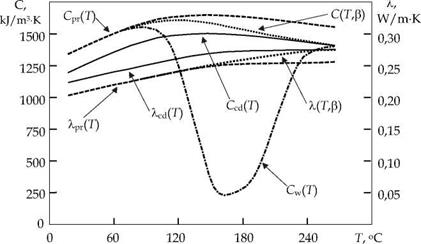
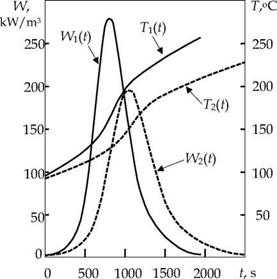
The results of experimental studies of the curing process and subsequent heating of the samples made of fiberglass plastic, as well as calculations of its characteristics are presented in Fig. 1-3.
|
Fig. 1. Thermophysical characteristics of fiberglass plastic at ys=0,51 |
The initial part of effective thermophysical characteristics Cw(T), Xw(T) (Fig. 1) before the beginning of intensive curing reaction characterizes thermophysical characteristics uncured prepreg Cpr(T), Xpr(T). The beginning of intensive curing reaction (on the figure is 110…120 oC) corresponds to a rapid decrease in the effective volume heat capacity Cw(T), because it includes the rate of evolved heat of cure reaction W(t) and it is in this part of the effective exothermic heat capacity. Effective thermophysical characteristics Cw(T), Xw(T) in the final stage of the experiment at a high degree of curing в merge with thermophysical characteristics cured material Ccd(T), Xcd(T), which corresponds to the transition of composite in the cured state. As seen from Fig. 1 the dependence of thermophysical characteristics of cured composite Ccd(T), Xcd(T) and uncured prepreg Cpr(T), Xpr(T) are equidistant curves. This allows the difference between the thermophysical characteristics cured composite and uncured prepreg AC and AX at the time of the beginning of the curing reaction, used for the calculation of thermophysical characteristics in the process of curing C(T, P), X(T, P). They are determined by thermophysical characteristics prepreg Cpr(T), Xpr(T) in the range from room temperature to the temperature of the beginning of the curing reaction, and above the temperature of the beginning of the curing reaction are determined by Ccd(T), Xcd(T) and AC, AX.
|
 1п{ф},
1п{ф},
[1/s]
8
![]()
6
The rate of evolved heat of cure reaction W(t) (Fig. 2) has a pronounced extremum, corresponding to the transition from a liquid resin to the viscous-flow state (gel point). With the increase in the rate of heating the extreme of evolved heat of cure reaction W(t) shifts toward higher temperatures. At the same time, the duration of heat generation and gelation time with increasing heating rate decreases. The area under the curve of the rate of evolved heat of cure reaction W(t) characterizes the full heat of the reaction Qf of curing reaction of the resin, and the ratio of the thermal effect Q to the full thermal effect of Qf corresponds to the degree of completeness of the process of curing or calorimetric degree of curing p.
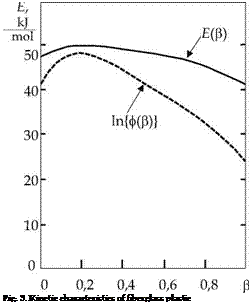
Kinetic characteristics £(P) and ф(Р) (Fig. 3) of the curing process are calculated from the rate of evolved heat of cure reaction W(t), at least of two temperature-time cycles. Rheological characteristics £ц and ~(P) are calculated by the change in the thickness of the samples L(t) under flowing out of the resin under pressure during curing.
Thermophysical, kinetic, rheological and dielectric characteristics of composites obtained in the experiment will be automatically recorded in the database of CMS. The dielectric characteristics e(f) and tanS(t) is then used to calculate the correlation dependence or the function of relationship Y(P) between the calorimetric and dielectric degree of cure, which is necessary for control of the manufacturing product process of composites in real time by controlling the degree of cure as well as to determine when to activate the pressure and completion of curing process (Dmitriev et al., 2010). The obtained parameters of the mathematical models are the basis for computer simulations of different situations in the curing process and calculate the optimal curing cycles of composite products of any thickness.