1.2 Single beam /-method
The determination of the samples density from the registration system is based on the measurement of y-radiation beam’s intensity attenuation. The beam is transmitted from a constant thickness sample. In collimated beam geometry, the intensity of y-ray beam is given by the exponential law Eq. (1). Consequently, the density of CM is given by the relation, for samples with known values of ц and x.
p = —ln(V) (12)
px ‘1
A typical set up of the radioisotope systems to study the low energy y-rays that transmitted through CM is given in Figure 1.
The y-ray coming from a source S is registered by the detector D. Collimator K1 is outside of detector. Inside the detector’s main body, the collimator K2, the scintillator of NaI(Tl) crystal, the photomultiplier (PMT) and the electronic block are being placed. The electronic block of radiometric data processing information, separates the informative pulses from the signal of the detector’s exit. Furthermore, it stabilizes the energy scale of the signals converter and measures the pulses containing information, on a given duration time. Finally, measurements’ results are presented on the PC’s screen.
K1 K2
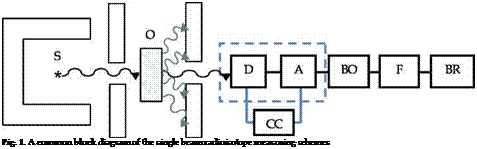 |
Ratio and system characteristics of collimators K1 and K2 or their absence, determines the required geometry measurements, which depends on the task and provides the most addictive signal on detectors output of parameters variation of the sample.
The detector is meant to realize the required measurement geometry. Additionally, it is used to achieve the registration of у-quanta, which are transmitted from the absorber. The radiation source and the detector have been placed in specific positions in order to ensure personnel’s safety. Furthermore, placing the radiation source and the detector in those positions provides the essential collimated geometry.
Density (volume density) p is for an object with a known thickness. In technical annexes Single beam у-method (SBGM) received adequate development (Chudakov and Anshakov 1982; Athanassiadis 1994). SBGM in static measurements are relatively simple in his mathematical description. Single-beam у-method is appropriate to apply when the sample thickness is x < 200 mm (Chudakov and Anshakov 1982). Optimal thickness of layer sample must, estimated on criterion of minimal statistical errors at a fixed measurement time, satisfy the condition (Chudakov and Anshakov 1982; Celi 1992):
![]()
![]() (13)
(13)
where:
ц – is the MAC and
P = p ■ I – is the surface density of a sample of thickness l and volume density p (Chudakov and Anshakov 1982; Celi 1992) concludes that SBGM allows us to control a change of surface density P=p4 in the direction of the heat axis. The conclusion is based on the fact that for the control of homogeneous flat samples of CM which have been high heated from one side and as a result of that heating affected changes in all three characteristics (ц, p, l) that are responsible for transmission of y-rays from an object, while the homogeneity of ц and p distribution characteristics is disturb in the direction of the heat. At the same time in the field of Ey > 100 keV of CM MAC does not depend of elemental composition. We assume that decomposition of CM impact only, on reducing its density while maintaining or slight change the thickness of sample.
(Chudakov and Anshakov 1982) report that by making use of y-densitometry methods along with the use of a single beam’s radiation technology, the researcher is allowed to check the surface density’s change in the address of light’s combustion of Composite Materials (CM). This is due to y-densitometry methods’ great simplicity. It holds true that the CM suffers high temperature effects. The development of a system providing the
possibility to dynamically control the measurement, allows the researcher to acquire data concerning the speed of mass’ loss in the unit of his heated surface. Furthermore, it offers the change to registrate the internal sample’s change of density and to construct its’ "behavioral" profile(Athanassiadis, Chudakov et al. 2008).

