Numerical studies on combined (compression and shear) buckling

The discussions and results on compression and shear buckling analysis will be done only for plate presented in figure AA9, having the same geometry and the orthotropic directions (a), thickness of the macro-layers (t) and plate lay-up according to Table AA1.

For analysis the calculus was done for various ratios a=q/p, that is {0.2; 0.4; 0.6; 0.8; 1}.

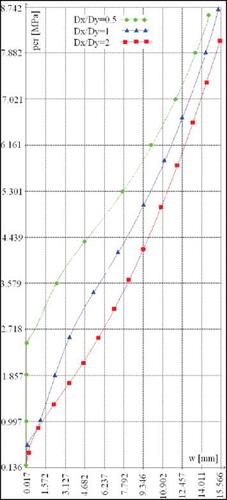
In figure AA16 the combined loading (shear and compression) buckling and post buckling behaviour of the plates with central delamination placed between macro-layers 1 and 2, for a=0.2 is presented.

According to the curves presented in figure AA16 the buckling load is decreasing since the value of the diameters ratio is increasing.

So, as it is seen in figure AA16, according to the plotted asymptotes, the buckling loads of the thin plates are placed in the domain 0.368 MPa < pcr < 2.634 MPa.

In the case of nonlinear model of the material behaviour, the buckling load (ultimate strength) was determined by Tsai Wu criterion, so that the degradation index (failure index) for tension and compression of the delaminated plates may be shown in Table AA7.

In the case of linear model used for material, the following conclusions can be formulated:

– For the values of in-plane loads lower than 40 MPa, the displacement values are increasing since the diameters ratio is increasing. This trend is due to the fact the transversal diameter is decreasing (since the delaminated area remains constant). Smaller transversal diameter means increasing of shear stiffness.

– In the case of the in-plane loading values bigger than 40 MPa, the displacement values are decreasing since the diameters ratio is increasing. This trend is due to the contact pressure between the layers in contact in the delamination, which is increasing since the loading force is increasing.

In the case of nonlinear material model (Figure AA13) the trend of the curves is so that the transversal displacement is increasing since the diameters ratio is increasing for the same in­plane loading, for a in-plane loading value under 25-40 MPa. For an in-plane loading value between 40 and 65 MPa in each case, a small instant jumping of transversal displacement is observed. This means that what is recover in plate stiffness after the increasing of contact pression in the delamination area, is lost due to the lamina damage occurring.

The buckling load determination is too difficult without the applying a graphical method, or the applying the Tsai-Wu failure criterion in the case of the general buckling not occurred till the first-ply failure occurring.

The first failure occurring in an element is based on the Tsai-Wu failure criterion, which provides the mathematical relation for strength under combined stresses was used.

The failure index is calculated in each ply of each element. In the ply where failure index is greater than 1, the first-ply failure occurs, according to the Tsai-Wu criterion. In the next steps, the tensile and compressive properties of this element are reduced by the failure index. If the buckling did not appeared until the moment of the first-ply failure occurring, the in-plane load corresponding to this moment is considered as the buckling load.

The lack of the criterion is referring to the anticipation of the real mode to occurring the cracking.

Taking into account the mathematical formulation, the Tsai-Wu failure criterion is easy to be applied. Additionally, this criterion offers advantages concerning the real prediction of the strength at variable loadings. In the case of shear buckling of thin plates, the ultimate strength of the delaminated plate is not depending on the position of delamination. For diameters ratio greater than 1, the ultimate strength in shear loading occurs only for traction fail.

Final remarks may be done. A very good postbuckling load carrying ability specific to light weight structures can be exploited to obtain high performance. Finite element analysis can offer more accurate analyses with a high degree of fidelity.

Since the plates included in the ship hull structure (so perfect or imperfect) are subjected to in-plane forces combined with transverse pressure, the buckling response of such plates is a basic concern in the design process. Furthermore, the presence of imperfections may weaken the load-carrying capacity of structures due to stiffness loss and cause an increase in stress concentrations in the imperfection area.

After the buckling, the composite plates, so perfect or imperfect, have a great capacity to be overloaded, so that the plate and finally the structure is not collapsed immediately.