In the theory of linear elasticity, the relation between the stress and strain in a solid body is usually described by Hooke’s law which postulates a linear relation between the two. The stress – strain relations for elastic anisotropic material have not been very well established as compared to those of the isotropic material in the classical theory of elasticity. The symmetry properties of the material, due to the geometric or crystallographic symmetry, may be defined by the group of orthonormal transformations which transform any of its triads vainto its equivalent positions. For the monoclinic symmetric second rank tensor, for instance, the basis elements can be found depending on the form invariant for the monoclinic system. Its form invariant expression, with v2 normal to the V1V3 plane, can be
written as
![]() °ij A11v1iv1j +A22v 2i v2] +A33v 3iv 3j +A31(v 3iv 1j + v1iv 3j)
°ij A11v1iv1j +A22v 2i v2] +A33v 3iv 3j +A31(v 3iv 1j + v1iv 3j)
where vai are the components of the unit vectors va (a = 1, 2, 3) along the material directions axes. The corresponding reciprocal triads satisfy the relations (Srinivasan, 1998)
vaiv. = 5.. a] 4
using (8) and orthonormalization by the well known Gram-Schmidt scheme, the four basis elements of the monoclinic system are obtained (Srinivasan, 1998):
T1 =-^ 5,.
4 V4 4
It is well known that for a symmetric second order tensor is of dimension six; an orthonormal basis set of six elements can be constructed. By taking cyclic permutation of {1, 2, 3}; the elements V and VI can be generated from IV in (10) as
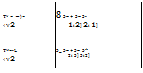 (11)
(11)
A complete orthonormal basis for the second rank symmetric tensor will be the set {I, II,…, VI}. The decomposition of is given in terms of these basis elements as
 |
|
where (o, Tk) represents the inner product of and the kth elements, т!], of the basis. Hence, the second rank symmetric tensor is decomposed into six orthonormal terms expressed in matrix form:
|
3 opp |
0 |
0 |
2(2on + o 33 – opp) |
0 |
0 |
||
|
o.. = i] |
0 |
1 opp |
0 |
+ |
0 |
2(-2o11- o 33 + opp) |
0 |
|
0 |
0 |
3 opp |
0 |
0 |
0 |
|
6("3° 33- opp) |
From (13), the second rank symmetric tensor, a.., is decomposed into six terms, each of which has a physical meaning. Also, the second rank symmetric tensor is virtually decomposed into two parts:
![]() o.. =i o 5.. +(o..-1 o 5..)
o.. =i o 5.. +(o..-1 o 5..)
i. 3 pp i. ч 3 pp i]
From (14), it is clear that the symmetric second rank stress tensor is decomposed into
1
spherical (hydrostatic pressure) part, — opp 5 , which is the first term of (13), and the
3 i]
1
deviatoric part, (o. — o pp 5^), which is the sum of the other five terms of (13). Hence, it is
shown that the method is able to decompose the symmetric second rank stress (and strain, in a similar manner) tensors into the spherical part which is connected to the change of volume without change of shape, and into deviatoric part, which is connected to the change of shape. This result is very well known in the literature. On the other hand, this method is introducing a new form of decomposition, which has a more featured and transparent
physical information. It is easily verified that the sum of the six decomposed tensors is the symmetric second rank tensor, a.. . Physically, each of the six tensor parts is associated with
a distinct type of deformation; the first part of (13) represents the spherical (hydrostatic pressure) effect, the second and third parts represent combined simple extension or contraction along the various symmetry axes. The second term could be, for example, stress of a non-uniform distribution of pure shear stress, which occurs in a long rod subjected to pure torsion, while the last three parts represent simple shearing in the symmetry planes. Besides, the deviatoric part of the stress tensor is decomposed into traceless tensors each of them is related to shearing which represents a general symmetric second rank tensor (stress and strain tensors). The results agree with previous studies considered as special cases of this general case, for instance, Blinowski et al. (Blinowski & Rychlewski, 1998) have decomposed a tensor of only shear into exactly identical forms to the last three terms of (13) for this specific case.


