Animation of L-Systems

In [166] and later in [164] Prusinkiewicz et al. introduced extensions for L – systems which allow for the animation of growth processes in static models. The most important extensions are the so-called timed L-systems, in which a number is assigned to each character and to each module. In the left side of the production the number represent the terminal age of a module, in the right side they represent the initial age. Within the animation, the global time will be counted up, and for the terminal age of the modules the appropriate productions are applied. The life spans of the modules start with their local initial ages and, if a terminal age is reached, the rewriting of that module occurs and new modules are produced.

While timed L-systems permit the animation of growth procedures, they do not permit communication of co-existing modules, which is nevertheless an important condition for the development of natural branching structures, as was already shown in Sect. 4.3. In [164] differential L-systems (DL-systems) are introduced that make this communication possible. Here L-system-like pro­ductions describe the topological modifications of the models, and differential equations describe the changes during the advance of time. According to their

Figure 5.10 Growth of Hieracium umbellatum (Courtesy of M. Hammel, P. Prusinkiewicz)

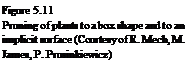(a)

possible. Two works were presented addressing this topic: [165] introduced environment-sensitive L-systems, and [144] proposed open L-systems.

In an environment-sensitive L-system, local aspects of the environment can af­fect the model. To model the effects, inquiry symbols of the form? X(x, y, z) with X = P, H,U, L are incorporated into the language. At the time of inter­pretation of the string, these symbols determine the position or orientation. In the first case (X = P) the values x, y,z represent the location, in the second case (X = H, U, L) the x, y, z represent the coordinates of the direction vector in the coordinate system. These values are passed on to user-defined functions, where their resulting values in turn affect the continuation of the string inter­pretation.

Using this mechanism, pruning can be implemented (see Fig. 5.11a). Another option is to limit the growth of the plant to the surface of other objects. The object is here defined as an implicit surface (see Fig. 5.11b).

In an open L-system, communication is no longer one-sided, but rather bi­directional. Those parameters connected with a communication symbol can be set either by the environment and passed on to the model or they can be set by the model and are passed on to the environment.

Communication was limited in the environment-sensitive L-systems to an in­quiry on position and orientation. Using open L-systems, communication mod­ules of the form? E(x 1, …,xm) for sending and receiving parameters are ap­plied. Here, the produced text is just like in normal L-systems, evaluated from left to right so as to designate the state of the turtle for each symbol. In this process, however, no character operations are implemented. If a communica­tion symbol is reached, the geometry-generating process sends a message to the environment modeling process with the following parameters:

■ address of the communication module in the string

■ values of xi,…,xm

■ state of the turtle (position, orientation)

■ type and kind of module on the right side of the communication module

The messages are read by the environment modeling process and worked on after conclusion of the interpretation of the string. The new values for the vari-

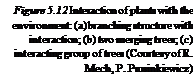(a)

ables x, are then sent back to the communication modules. Here the addresses of the communication modules are used. In this way, theoretically the entire information in the plant can be passed on to the environment; usu­ally, however, only a part of the information is needed.

In Fig. 5.12a this mechanism is used for modeling a branching structure. The smaller branches interact with one another, in order to not exceed a defined density. This follows the branching model of Honda from Sect. 4.3 and is in­fluenced by the light. If two trees are planted next to each other, their crowns form one system (Fig. 5.12b). A tree group can likewise be modeled as an in­teracting system (Fig. 5.12c). The appropriate systems are relatively large, and are described as in [144].