Cross-Hatching Using Half-Toning

Halftoning procedures also offer the option of generating a cross-hatching with short lines on the surface. Here the standard algorithms are modified: instead of generating points, now lines are created. In [36] this is realized through a mod­ification of the classical Floyd-Steinberg algorithm [65]. Usually the algorithm scans the image per line from top to bottom, sets black and white pixels into the image to be produced, and measures the grayscale value error that hereby occurs. This error is then distributed to the neighboring pixels.

A modified procedure for lines uses another error term[12]. Unfortunately, only short lines can be used, since the Floyd-Steinberg algorithm is a locally work­ing method that consequently produces larger errors when working with long lines. The directions of the lines are modified according to the surface in such a way that a spatial impression is created. Markosian et al. present a similar method in [128].

Figure 11.16 shows an application of the modified Floyd-Steinberg method on the trunk of tree I. The silhouette was rendered using the depth-difference algorithm, and the cross-hatching with the modified half-toning method. In part (a) we see a realistically rendered image; part (b) shows a model without textures and with modified surface attributes; part (c) displays the result for which approximately 2000 lines with roughly equal lengths were used.

Using the half-toning method, cross hatchings with short lines can be produced. A further, completely differently working procedure allows us also to create longer lines. This is described in the following. With the method a large number of different geometric models can be represented as line drawings.

Here we again refer to the principle differences of shadings using short and long lines. While the former can be produced using local procedures, and must give little consideration to the geometry, the latter are to be generated only using global methods and are affected strongly by the geometry. Often the form of the hatching lines is the strongest visual hint to the form of the geometry and must therefore be selected accordingly.

The starting point for the algorithm is the observation that in many drawing styles the cross-hatching lines can be understood as intersection curves be­tween the object and a number of parallel planes. This was already addressed previously, and also demonstrated in the examples from Fig. 11.8. The observa­tion leads to a good algorithmic approach, since intersections between planes and surfaces can be computed in most cases efficiently. The approach offers in addition a number of further advantages in comparison to the methods dis­cussed in Sect. 11.4.

■ Instead of producing cross-hatching curves pixel by pixel, the curves are generated as a whole, and therefore in the subsequent processing they can also be drawn as a whole. This is important if artistic line styles are used because these are difficult to combine.

■ For a number of models, and in particular also for tree skeletons, the ori­entation of the intersection planes can be computed from the geometry. In this case, the method is completely automatic and can be used, for example, within animations.

■ Depth-buffer-based procedures or similar, which are implemented using raytracing, often produce visual artifacts through numeric problems. Many of these problems are avoided using the algorithm introduced in the next section due to the combination of analytical and pixel-based operations of the graphics hardware.

Just like half-toning, the method uses a reference image of the object. In this case it is a computer-generated rendering of the three-dimensional geometry in a view chosen by the user. Similar to the approach of Leister, here different light effects, such as reflection and shadow casting, can be introduced, since the method accepts any computer-generated rendition as an underlying image. The lines of the cross-hatching then represent the illumination at each point through thickening and blackening.

In the next step, the object is segmented. For doing so, the model parts that are to be illustrated by a cross-hatching are extracted. With an underlying 3D model the parts mostly correlate to geometric parts of the entire object. These are then viewed and processed individually. If this correspondence is not given

the 3D model must be preprocessed accordingly. In each case this step is to be implemented manually, since it is a design decision that depends on the desired visual effect.

Each of the parts is now intersected with a set of planes. The number and align­ment of the planes are either manually adjusted or computed automatically. Aside from the main alignment of the planes, they can also be rotated slightly from plane to plane in order to follow a curved object. In the last step the inter­section lines are projected onto the drawing surface, and their thicknesses are varied according to the grayscale value of the reference image.

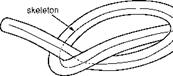
For many models the definition of the intersection planes can be automated. Here the skeleton of the geometry is determined that consists of a line or a graph within the geometry, and which also includes topological and geomet­ric attributes of the object. The topological information is stored in the graph structure, and the geometric information in the lengths and angles of the edges [59]. Figure 11.17a shows the result of the skeletonization of a bent hose. The skeleton remains inside the hose and approximates its midaxis. A spline inter­polation is used to compute the edges that are rendered as a smooth curve.

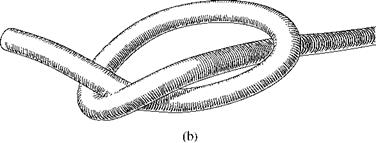
In the next step, the planes are aligned vertically to the skeleton curve, and are then used for the production of the intersection lines. The result can be seen in Fig. 11.17b; the line thickness is here controlled by the grayscale value of the image. In the next paragraph we describe this.