 |
 |
To model a terrain, bivariate versions of sine or noise functions are defined. The midpoint displacement, instead of lines, is now applied to triangles. A triangle, for example, is divided by finding the midpoints on each of the sides of the triangle and connecting its consecutive midpoints. Connecting the consecutive midpoints of the edges will divide any triangle into four smaller triangles.
If, however, a bivariate noise function is used, then it can be combined from three parts,
B(x, y) = Bx(x) + By(y) + Bxy(xy), (7.6)
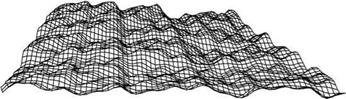
thus only out of two functions Bx(x), By(y), and a mixed term. An image generated with such a function is shown in Fig. 7.3.
The individual noise functions again evolve out of a sum of sine functions, in this case, seven functions, in combination with a Holder exponent H = 0.4, as well as r = 0.45 and /0 = 1,/ = /i-1 + 0.7. The illustrated area has a width of 2n. The image shows an already relatively natural-looking elevated field, which drops slightly to the right due to the influence of the low frequencies. Such a terrain is also termed a homogeneous fBm terrain (fBm: fractional Brownian motion).
Figure 7.4 demonstrates the influence of the fractal dimension on a height field. Here the ruggedness and also the fractal dimension rises linearly from left to
right. This variation of the fractal dimension approaches the solution to a problem we saw in conjunction with the earlier procedures: due to the uniform fractal dimension, the terrains came across as looking too bland.
|
|
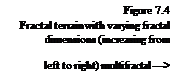Kenton Musgrave [52] developed two methods for varying fractal dimensions locally in a terrain. Due to their attributes, both methods are denoted as multifractals, though that is only because the computer graphics community handles the term rather casually; actually, the synthesized objects are not fractals in the strict mathematical sense.
A simple solution for the generation of multifractals is offered by the height – dependent variation of the fractal dimension. Natural mountain ridge outlines are usually much more rugged than the outlines of valleys, since erosion processes affect the landscapes differently. Musgrave replicates this using height – dependent control of the fractal dimension. For each point, through synthesis with low frequencies, the actual height is assessed. The higher frequencies are only added at the points that exceed a certain height.
In his second method, Musgrave tries to produce washed-out and thus soft valleys of all depths by scaling the values of the higher frequencies with the preceding ones. Although this method does not yield the desired effect, the results are interesting terrains with alternating ruggednesses. A collection of examples is to be found in [52].
Given these ideas, Musgrave has been developing for some years a system for the automatic production of landscapes. “MojoWorld” produces whole synthetic planets that over a Web interface that can be combined by different users into a synthetic galaxy. However, this is only possible because for a fractal description the parameter set of a whole planet can be reduced to a few kilobytes; nevertheless, illustrations such as Fig. 7.5 can be produced with not too much effort.
