The local lighting methods utilized during the early years of computer graphics completely ignored indirect lighting in a scene. The amount of light was controlled only by the radiance of the light sources and direct illumination, where the reflection was approximated using different terms. The situation is illustrated in Fig. 9.2.
|
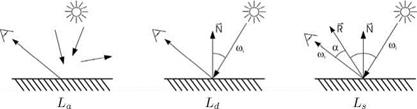
Using the ambient light term La, a base illumination of all surfaces is implemented. The amount of this light is calculated using a base amount of light in space, Lg, and a material parameter ka є [0… 1], which is the ambient reflectivity of the object.
La = ka Lg. (9.1)
The second term of the approximation designates the diffuse reflection of the light by the object. It is computed using the diffuse light term Ld. Examples of diffuse reflectors are materials such as chalk and concrete. The quantity of the reflected light depends here solely on the angle between the vector ші from the light source i and the surface-normal N, multiplied by the diffuse reflectivity kd. With the diffuse reflection, light is distributed evenly in all directions.
Glare lights on the object surface result from so-called specular reflection Ls. This value describes shiny surfaces. A mirror reflects the light of a light source i only in the reflection direction R; a shiny object, a so-called non-perfect mirror, reflects the light into the close neighborhoods of this direction also.
The function cos(R, J)n = cos(a)” describes, in dependence of the material parameter n, how fast the reflected light in the environment of reflection direction decreases, and thereby determines the size of the glare lights on the object surface. The term J is here the direction of the virtual viewer. The specular term is then given by
Ls(J) = ks cos(R, J)n Li. (9.3)
The sum of the three terms for each pixel gives a visual approximation for direct lighting. Together with m light sources, the approximation formula is given by:
L(j) = La + Ld + Ls
m
= ka Lg + ^2 Li [kd cosJ N) + ks cos(R, J)n^ . (9.4)
i=1
In physical reality the situation is, however, more complex. Thus, the material properties depend on the respective position on the object, and must accordingly be included in the equation. Also, the reflection characteristics are substantially more intricate and can be approximated only for some materials in the way presented so far. Finally, an object may potentially illuminate all others, which produces the global interaction already addressed.
