To model branching structures, often tree-like data structures are used. We saw this already in some procedural methods in Chap. 4. In the case of L-systems, the tree is represented as text in linear form. Iterated function systems can, as demonstrated above, likewise be represented as trees that encode the transformation rules for points.
|
|
|
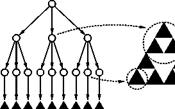
Since these data structures most likely occupy a lot of space, depending upon the complexity of the objects, it is meaningful to introduce compression techniques. One option is to represent the produced geometrical primitives canonically and to place them in a tree using relative positioning data. In this case, subtrees, which produce the same objects in different places, can be represented by just one subtree, whose root nodes may have several fathers. The tree becomes in this case a directed acyclic graph (DAG). The process is called object
instancing, and was used for the first time by Ivan Sutherland in his system Section 5.12
Sketchpad” [216].
A subset of L-systems, as well as the iterated function systems, can efficiently be represented by such graphs [166]. Kay and Kajiya [108] applied this technology for the first time to fractal objects. Here, cycles develop in the directed graphs, and the object can be described in arbitrary detail.
Hart and DeFanti [84] describe efficient methods for the modeling and representation of cyclic object instancing hierarchies. Figure 5.16a shows the tree hierarchy for modeling an approximation of the Sierpinski triangle from part (b). The leaves of the tree are the geometric primitives; the internal nodes represent relative transformations and combine the produced geometry.
 |
 |
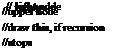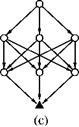
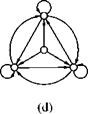
In Fig. 5.16c the graph was converted into a directed acyclic graph that also represents the object. If cycles in the graph are permitted (Fig. 5.16d), then the fractal object can be represented arbitrarily exactly and a Sierpinski triangle is yielded. Hart [83] provides a more detailed description of the graph in Fig.
object top
{ merge: up, left, right
}
Likewise in [83] the transformation of a subset of L-systems and of RIFSs into the cyclic graphs of the object instancing paradigm is described. The conversion of the RIFS is executed via the transformation of each function into a
canonical object; the RIFS graph is transferred directly into the cyclic graph of the object hierarchy.
The already-mentioned possibility of converting L-systems into RIFSs (see [166]) allows us also to convert them into the object instancing paradigm. Hart sketches furthermore a direct conversion method for strongly recursive branching structures. However, a general transformation method seems not to exist.
Instancing is possible within a branching structure as well as in a compilation of plants. Thus in Chap. 8 instancing is applied for the modeling of plant communities. Instead of defining each plant individually in a lawn, a small number of prototypes is stored and copied as needed. This permits a strong reduction of the needed disk space, and at the same time makes the scenes easier to handle. A substantial difference to the method described here is the approximate character of instancing. A number of similar objects are represented visually by only one prototype. “Approximate instancing” can be used for natural objects on many levels, without substantially affecting the visual appearance of the results.
Figure 5.17
Tree model generated using a cyclic CSG-graph (Courtesy of M. Gervautz and C. Traxler)
