Ten years after their first work, Honda et al. [92] examined how a branching procedure can be controlled by rule mechanisms. They found that with plants that have dense branching structures, no overlapping of the branches occurred, therefore there had to exist a mechanism by which overlapping could be prevented locally. The simulation of such local control mechanisms is the aim of this work.
|
(d) (e) (f) |
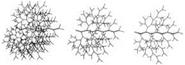
The models shown here are two-dimensional, and two kinds of regulations are analyzed: In the first model a purely sympodial branching is implemented, and is only then executed if no other branches project into the circle drawn around the branch point. The circle has a constant size for all branching orders. Depending upon the radius, different branching patterns emerge, as shown in Fig. 4.6a-c. The second procedure looks at how the branching characteristics are modified if during branching, the successive growth is given different growth rates (flow rates). These rates indicate how much material for the growth stimulation of the plant flows into the two sub-branches of each branch. In this way, tree-like growth can be simulated. Two growth rates fi, f2 & [0..1] are defined. During growth, discrete quantities of material, relative to the values, are distributed into the branches. The results are shown in Fig. 4.6d-f.
Here we are dealing with a typical representative of exogenous procedures, in which growth is determined by external factors, and which therefore must have appropriate data structures in order to efficiently support spatial interactions, especially, if we are managing complex branching structures. In the case at hand, this was not yet necessary due to the simple models.
