Loads exerting on NASC will be transferred to fibers through matrix, and the mechanism relates to constitutive equations and mechanical behaviors of fibers, matrix and interface phase. According to the thermo-viscoelastic theory and the shear-lag theory of fibrous composites, a micromechanical model of a single fiber cylindrical cell, which includes a fiber, the matrix and their interphase, is established.
1.6 A micromechanical model of NASC
 |
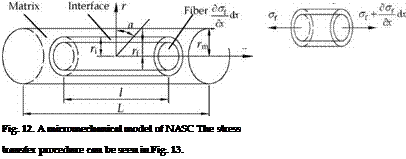Fig. 12 illustrates a micromechanical model of NASC, where l is the fiber length, L the matrix length and L~l. The volume content of fiber is Vf.
Fig. 13. Micromechanical stress transfer in NASC
When the single fiber cylindrical cell is only subjected to the tension load along the x axis, the circumferential and the radial stresses in the model are much less than the axial stress, and they can be neglected.
The equilibrium relationship of the stresses shown in Fig. 13 can be expressed by
do f (*) (15)
dx rf
 |
 |
 |
 |
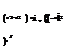where cr(x) is the axial stress in fiber and Tif(x) is the shear stress on fiber surface. The axial shear stress in matrix Tm(r, x) can be expressed by
where Tim(x) is the shear stress at the interface boundary near the matrix.
 |
 |
 |
The shear stress in the matrix is a time dependent physical quantity, and it holds the following relationship with the shear strain.
where um(r, x, t) is the axial displacements of the matrix, and JTm(t-s) is the creep function. If the bond of both the matrix and the fiber with interface ideally, the axial displacement of the matrix can be expressed by
r (r Л [2rmln(rlr.)-(r2-r2)]г: .t
, (r, x,t) = U. (rf, x,t) + – LlnI – L ]Tif (x, t) + —————— TT-2—— П~ J0- JTm ( – S)dT. m (x, t)
h Vrf J 2[r;2 – r2) Jo
 |
 |
The strain of the matrix £m(r, x, t) holds
 |
 |
According to the viscoelastic theory, the shear stress of the matrix Tif(x, t) holds
du, (rf, x,t) du{ (rf, x,t) of (x, t)
Considering u, (rf, x,t) = uf (rf, x,t), —— ^——— — =——————- = e{ = —^—-+ afAT and
dum (rm, x,t)
 |
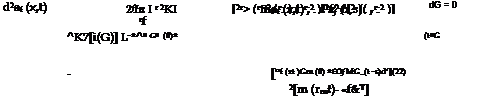dx
 |
 |
Eq. (22) is the micromechanical model of NASC which expresses the stress transfer regularity among the matrix, the fiber and their interface.
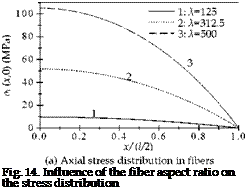
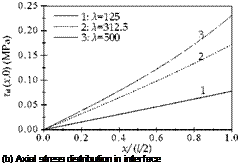
The stresses in fibers and interface are illustrated in Fig. 14, where the coordinate x represents the axial distance from the midst (x=0) to the end (x=l/2) of the fibers. Fig. 14(a) reveals that the axial stress in the fibers Of reduces from the midst to the end, and with the increasing aspect ratio X, Of at the fiber end increases. Fig. 14(b) illustrates the shear stress distribution in interface at the fiber side, and the shear stress increases from the midst to the end.
