A composite material is a medium comprised of at least two different material phases: a matrix (host, bond) material and inclusions. A matrix is typically a polymer dielectric, while inclusions may be either conducting or non-conducting, and may have their own dielectric and magnetic intrinsic properties. Depending on how many phases there are in the mixture, composites can be biphasic or multiphasic. The material phases may be intrinsically isotropic or anisotropic, depending on their crystallographic structure or morphology. The latter is determined by synthesis or manufacturing process specifics, such as temperature and pressure regimes, presence of catalysts, doping ions, and the kind of mechanical processing that was applied (milling, extruding, moulding, or pressing). Inclusions may be of identical or different sizes and shapes, and may possess the shape (form) anisotropy. In the general case, the axes of shape anisotropy do not necessarily coincide with crystal or texture axes of their constituent material. Inclusions inside the host matrix may be arranged in a regular periodic 3D or 2D structure, or may be randomly dispersed. They may either be homogeneously distributed over the space, in a the plane, or forming clusters. As for orientations of non-spherical or intrinsically anisotropic inclusions, their main axes may be all aligned, or dispersed statistically according to some distribution law. Inclusions may have any orientation with equal probability in 3D or 2D space, or may fall within some spatial angle, forming a structure with a certain rate of order.
A composite is an inhomogeneous structure. However, it can be characterized by effective electromagnetic parameters, obtained through averaging, or homogenization (Von Hippel, 1995), if sizes of inhomogeneities are much smaller than the wavelength. Any existing homogenization theory tries to ascribe effective parameters to a mixture of different phases, providing mixing rules (Sihvola, 1999). A mixing rule is an analytical formulation that describes an effective parameter as a function of frequency and concentration. Hence, it is very desirable that effective permittivity and permeability of a composite would be governed by the same mixing rule. For example, it has been recently experimentally observed that ^ and £ of composites with multi-domain magnetic inclusions may be governed by analogous (dual) mixing rules (Rozanov et al., 2009).
There is currently a multitude of mixing rules in the literature based on different homogenization theories and approaches. They are applicable to different types of mixtures, rate of generalization, and depend on which parameters are homogenized, and what their limits are. This is not aimed at a review of all existing homogenization theories and models. A good review of existing mixing rules can be found in the current literature (Landauer, 1978; Sihvola, 1999; Diaz et al., 1998) and references therein.
There are a few most widely used mixing rules, which are briefly reviewed herein. The first is the Maxwell Garnett (MG) formulation (Maxwell Garnett, 1904, 1906), which results in the lowest estimate of the effective parameter. The MG rule in terms of the relative dielectric or magnetic susceptibilities, expressed through the corresponding dielectric and magnetic contrasts between inclusion and host materials
and effective parameters of the mixture and the host
can be written as
^_=_a. (3)
1 + пв 1 + па
The parameter p is the volume concentration of inclusions in the composite. The parameter n describes effective depolarization or demagnetization factors, often called „form factors" of inclusions (Landau & Lifshitz, 1960). The form factor for calculating permittivity and permeability should be the same. This shape factor is n=1/3 for the particular case of spherical inclusions.
The second widely used theory is the Bruggeman symmetric rule (BSR), which is also known as the effective medium approximation (EMA) (Bruggeman, 1935, 1936), as is
For the permittivity of a metal-dielectric mixture, the BSR is conventionally considered the most suitable theory, because it allows for predicting the percolation threshold pc (McLachlan, 1990). The latter is the concentration at which the composite turns from a non-conducting to a conducting state, and where the real part of effective permittivity of the mixture tends to infinity. As follows from (4), the percolation threshold should be equal to the average form factor, pc = n. However, even for a mixture of spherical particles with n=1/3, pc may vary over a wide range, since the percolation threshold is associated with interactions between inclusions and matrix. It has been experimentally shown, for example, that in composites filled with carbon black inclusions of almost identical spherical shape, but with different polymer host materials, the percolation threshold varied from about 5 to 50% volume fraction of inclusions (Miyasaka et al., 1982). The experimental data do not agree with the BSR prediction of pc * 30%. Moreover, even for a composite containing carbonyl iron powder (CIP) with almost perfect spherical inclusions, the experimentally obtained effective form factor both for permittivity and permeability may significantly deviate from 1/3 (Osipov et al., 2002). This means that the BSR may not be applicable for predicting properties of magnetic composites. The third important mixing rule is the the Bruggeman asymmetric rule (BAR), or 1/3-power rule (Bruggeman, 1935; Hanai, 1960; Neelakanta, 1995)
(в+1)) -(1 – p )=ав. (5)
This rule is fit to the composites of randomly distributed spherical inclusions, and can be applied to both dilute and dense mixtures.
The Landau-Lifshitz-Looyenga (LLL) formula (Landau & Lifshitz, 1960; Looyenga, 1965; Dube, 1970),
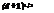
![]() (6)
(6)
plays a special part among the mixing rules. The LLL formula is rigorous at low inclusion – matrix contrast a << 1, and, hence, at high frequencies (ш ^ от). Thus any mixing rule should converge to the LLL limit at the high frequencies. This is important, because predicting frequency dependences of the material parameters must include the high – frequency region. For example, it can be shown that at n = pc = 1/3, the BSR satisfies the LLL high-frequency limit. However, the parameters pc and n are of a different physical nature: the percolation concentration pc describes collective properties of inclusions, while shape factor n is an individual characteristic of an inclusion related to its depolarization or demagnetization at the boundary surface. This means that in a physically meaningful mixing formula these two parameters should be uncorrelated "free" fitting parameters for any particular composite. Such splitting of pc and n as two independent physical properties can be found in a formulation proposed by Odelevsky (Odelevsky, 1951) for calculating static effective permittivity of a metal-dielectric mixture,
The formula to describe static magnetic properties of composites containing ferromagnetic inclusions in a dielectric host is analogous to (7)
,, _ – і + V ■ Pc ■ (A -!) (8)
n (c – V), – 1)+ Pc
Odelevsky’s formulas (7) and (8) fit experimentally obtained static data (Rozanov et al., 2009), and it can be used for finding intrinsic permeability and permittivity of inclusions (without any host material). This is very important, since in majority of cases these values are not known and cannot be found by any other methods, especially, intrinsic permeability of magnetic inclusions, which is different from the bulk materials. The latter significantly depends on the way of crushing the bulk magnetic material and the crush parameter ^, which is a ratio of an average gap between magnetic particles in the crushed bulk material to an average size of a magnetic particle, or grain (Tsutaoka, 2003). At low frequencies (ш ^ 0), Odelevsky’s formulas (7) and (8) converge to the corresponding MG formula (3) for pc = 1. When n = pc = 1/3, formula (7) for effective permittivity becomes equivalent to the BSR (4), but formula (8) for effective permeability never turns to (4). Moreover, both (7) and (8) do not satisfy the LLL limit at high frequencies (ш ^ от). For this reason, Odelevsky’s theory is applicable only for static parameters.
The mixing rules (7) and (8) are formulated for a quasi-static assumption, which means that the inclusion size is much less than the shortest wavelength in the composite. Hence the frequency dependence of the effective material parameters of the mixture is associated with frequency dispersion in its ingredients. If the host martix is almost non-dispersive, the frequency dependence of the mixture will be totally determined by the frequency responses of the inclusions.
There are also complex mixing rules, which are based on cluster theories, e. g., (Sheng, 1980; Hui & Stroud, 1986; Musal et al., 1988; Doyle & Jacobs, 1990). They describe different groups of inclusions (clusters), using different mixing rules depending on their applicability. Then separate clusters are mixed using some other mixing rule at the higher level of homogenization. In some cases, these cluster theories provide good agreement with
experiment, but due to their complexity, choice of partial mixing rules is a matter of art rather than science, and there are no general recommendations that could work for any type of a composite.
Any mixing rule should describe effective permittivity and permeability using the same mathematical formulation due to the duality of є and ц. However, existence of numerous mixing rules in the present-day literature indicates that there is no unique rule that is be applicable for describing simultaneously dielectric and magnetic properties of magnetodielectric composites over a wide frequency range. Researchers make attempts to model effective properties for particular cases of mixtures, and any mixing theory has its applicability limitations. Thus, for an important case of composites filled with ferromagnetic metal powders, currently there is no standard unified and experimentally validated mixing rule to calculate dependences both of frequency and concentration.



