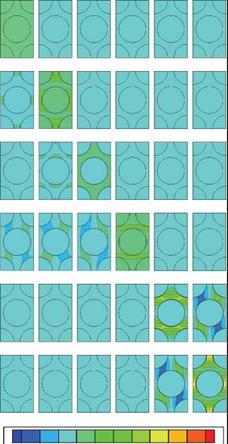
The influence matrix and thermal superposition vector can be extracted from the same set finite element analyses used to determine the effective lamina properties. It should be noted that both the influence matrix and the thermal superposition vector are field variables. That is, each specific geometric point within a representative volume element yields a unique influence matrix. Presented as field variables, the terms of the influence matrices and thermal superposition vectors are illustrated graphically in Figures 4 and 5, respectively.
The micro-strain field can be extracted at every node or integration point within the representative volume element. The enhanced strain field at every point within a volume element can be used in a point failure criteria. Alternatively, a smaller set of points can be selected for examination in order to increase computational efficiency. The same method is applicable for a stress based criteria whereby the stress state at a point is determined from the strain state through the appropriate constitutive relationships.
 |
 |
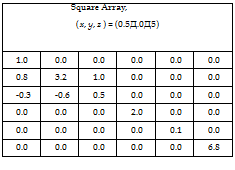
In the current example, a single point is used to provide a numerical illustration of the micromechanical enhancement process. Tables 4 and 5 contain the influence matrix and thermal superposition vectors respectively. The data is extracted for both the square and hexagonal representative volume elements at the point (ei, e2, e3) = (Li/2, L2, L3/2). Although both points represent locations that are midway between two fiber centers, the influence matrix and thermal superposition vectors are different for the two representative volume elements. This shows the effect of packing geometry on the local strain fields and the need for a comprehensive understanding of the underlying geometry contained in the composite material.
Table 4. Influence matrix for both representative volume elements at the selected location
![]()
|
|
|
Fig. 4. Influence matrix fields for both representative volume elements, square and hexagonal
|
|
||||||||
|
|||||||||
|
|
|
|
|
|||||
|
|
|
|||||||
![]()
|
|
|
|
![]()
![]()

Fig. 5. Thermal superposition vector fields for both representative volume elements, square and hexagonal