1.2.1 Theoretical aspects
The effective atomic number Zf and the density p are among the parameters which characterize the technological, and exploitation attributes of materials and their derivatives. Particular characteristics, like the no-contact measurements, the high productivity, the conformity, and the relatively simple instrumentation needed, have extended the use of methods based on photon radiation transmission to the radioactive control of materials (Athanassiadis 1994).
The creation of methods for no-contact, non destructive control of Zef and density p of localized areas of the material samples will allow the clarification of the physical and mathematical models of degradation of the composite materials under conditions of high temperatures. For the determination of Zeff, it is necessary to use detectors with high energy resolution, due to the need to distinguish between spectrum lines of coherent and incoherent scattering of y-rays (Athanassiadis 2009).
The analysis of physical and chemical characteristics of materials via the determination of change in the effective atomic number Zf can be performed by measuring the ratio of elastically Nr (Rayleigh) to the in-elastically Nc (Compton) scattered y-rays intensities.
The total effective atomic cross-section aR for Rayleigh scattering approximately is:
![]() Zn
Zn
= —
1 Em
where:
ci – constant for the particular scattering angle;
Z – atomic number;
E – energy of incident photon; n, m – certain constant numbers.
The effective atomic number and the other parameters are independent from energy (Perumallu, Rao et al. 1985). The values of numbers n, m depend from the type of process. Total effective atomic cross-section crC for Compton scattering approximately is:
![]() Z
Z
= c2 —
2 Em
Dividing the total atomic cross-section aR for the Rayleigh scattering (14) with the total atomic cross-section aC for the Compton scattering relation (15) we have the relation between the scattering cross-sections that is (Manninen, Pitkanen et al. 1984):
![]() ^ = c3Zn
^ = c3Zn
where c3 is a constant for the particular photon energy.
![]()
|
||
|
||
|
||
|
||
 |
||
|
||
|
||
If an angle d is smaller than the "characteristic" angle (d<d0), then if the "characteristic" angle d0 approaches 0, the scattering ratio is proportional to Z2 and does not depend on the energy E. It is important to note that the ratio gr/gc increases with increasing atomic number Z and decreasing energy E.
Taking the Thomas-Fermi approach into consideration, for the distribution of electron, the differential cross-section of the coherent scattering can be written as (Manninen, Pitkanen et al. 1984):
 (21)
(21)
V 32П ) 2mc2
In this approach the differential cross-section daR/dn is proportional to Z3, however, this is only correct for scattering angles bigger than the characteristic angle (Manninen and Koikkalainen 1984; Leichter, Karellas et al. 1985).
Based on the angular frequencies of incident photons ш1 and scattered photons wJJ the Klein-Nishina formula is approximated by the relation (Manninen, Pitkanen et al. 1984; Perumallu, Rao et al. 1985):
![]()
![]()
![]() d&KN _ ( ( &20_)
d&KN _ ( ( &20_)
dQ. V dQ. )Th V m1 )
and for the incoherent scattering:
daC (d&’ (m° ‘j z
dQ ^ dQ )Th ^ m1)
Assuming that the scattering angle is not smaller than:
sin /X – 20nm 1or > 2 A° 1
Dividing (21) with (23):
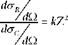 (25)
(25)
where k – numerical factor.
Equation (25) is acceptable only for specific values of energies Ey < 100 keV, scattering angles smaller than d0 and elements with 6 < Z < 83 (Manninen, Pitkanen et al. 1984; Athanassiadis 1994).
From this relation, one can deduce the parabolic dependence of the Rayleigh to Compton scattering ratio (R/C) from the atomic number of the scatterer (Manninen and Koikkalainen 1984; Duvauchelle, Peix et al. 1999; Manohara, Hanagodimath et al. 2008; Athanassiadis 2009).



