 |
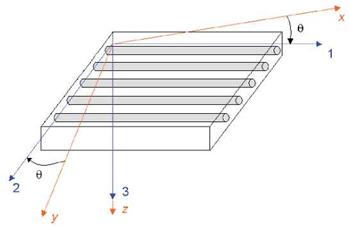
In high-performance composite structures, structural components are manufactured mainly from unidirectional fibre-reinforced plies, where the ply axes are identified in the principal coordinate system with numbers 1, 2 and 3. Whereas, the laminate axes are identified in the global coordinate system (Cartesian coordinates) with letters x, y and z (Jones, 1999 & Saarela, 1994). The 1-axis and z-axis are combined into a single axis (Figure 8).
The Young’s moduli £i, E2, E3 and the shear moduli G12, G23, G13 of the unidirectional ply
determined from experimental tests will become E1, E2 , E3 , G12 , G23 , G13, respectively. In relation to this orientation and for a unidirectional fibre-reinforced ply, the eco-efficiency factors related to the engineering constants for the linear-elastic mechanical behaviour may be defined in the principal coordinate system as (Attaf, 2008):
E G’ E E-
J = —L, J j with —L = – І – (i, j=1,2,3 and i^j) (9)
Ei Gij Vij Vji
where Ei, Ei are classical and sustainable Young’s moduli in i-direction (i=1, 2 and 3),
Gij, Gij are classical and sustainable shear moduli in the i-j plane (i-j=2-3, 3-1 and 1-2),
Ji, Jij are the eco-efficiency factors of Young’s and shear moduli, respectively and, vij is the Poisson’s ratio for transverse strain in the j-direction when stressed in the i-
direction. For this value, it is important to note that no attempt was made to investigate the sustainability of Poisson’s ratios. Their influence is beyond the scope of this analysis. According to these assumptions and generalized Hooke’s law, the strain-stress eco-relations for an orthotropic material in the principal coordinate system (1,2,3) may be written in compact matrix form as:
6×6 (6 rows by 6 columns). The components Sij = Sji are defined as:
|
"r—^ II |
S12 = – V12/ |
E1 |
S13 = ~V13I E1 |
S14 |
= 0 |
S15 |
= 0 |
S16 |
= 0 |
|
|
S21 = – У21І |
E2 |
S22 = 1E2 |
S23 = – V2^l E2 |
S24 |
= 0 |
S25 |
= 0 |
S26 |
= 0 |
|
|
S31 = – V31 / |
/E3 |
S32 = – V321 |
^3 |
S33 = 1E3 |
S34 |
= 0 |
S35 |
= 0 |
S36 |
= 0 |
|
S41 = 0 |
S42 = 0 |
S43 = 0 |
S44 |
=V G23 |
S45 |
= 0 |
S46 |
= 0 |
||
|
Ul. • II 0 |
S52 = 0 |
О II CO . • LO |
S54 |
= 0 |
S55 |
=V G13 |
S56 |
= 0 |
||
|
S61 = 0 |
S62 = 0 |
О II CO . • 40 чл |
S64 |
= 0 |
S65 |
= 0 |
S66 |
= V G1 |
Also, the eco-stiffness matrix of the ply may be obtained by the inverse of the ecocompliance matrix. Thus, we can write:
When using the eco-stiffness matrix, the stress-strain relations can be obtained by the inverse of Equation (10). Thus, we obtain:
Since orthotropic fibres have almost the same characteristics along 2- and 3-axis, the 2-3 plane is considered to be a plane of symmetry and the three-dimensional 123-coordinate system will be reduced to two-dimensional 12-coordinate system. Thus, Equation (12a) becomes:
where (M12 = {m m2 t12}T, {s}12 = {e1 s2 y12}T are the stress and strain vectors in 12-
12
columns).
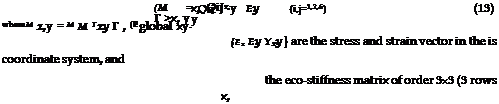 |
Using the transformation matrix, Equation (12b) may be written, after some rearrangements, in the global xy-coordinate system as:
by 3 columns). The components Qij = Qji (i, j = 1, 2, 6) are functions of the fibre orientation
angle, 0 and the orthotropic elastic eco-moduli of the ply. By letting C=cos 0 and S=sin 0, the eco-stiffness components are defined in the global xy-coordinate system as:
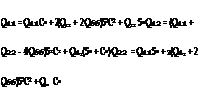 Q16 = (Q11 – Q12 – 2 Q66 )SC3 + (Q12 – Q22 + 2 Q66 )S3C Q26 = (Q11 – Q12 – 2 Q66)S3C + (Q12 – Q22 + 2 Q66 )SC3 Q66 = (Q11 + Q22- 2Q12- 2Q66)S2C2 + Q66(S4 + C4)
Q16 = (Q11 – Q12 – 2 Q66 )SC3 + (Q12 – Q22 + 2 Q66 )S3C Q26 = (Q11 – Q12 – 2 Q66)S3C + (Q12 – Q22 + 2 Q66 )SC3 Q66 = (Q11 + Q22- 2Q12- 2Q66)S2C2 + Q66(S4 + C4)
With these ecological considerations, the constituent equations for laminated composite structures can be derived using the classical lamination theory (Jones, 1999).
1.6 Constitutive eco-equations of laminates
When the environment and health impacts besides quality are taken into consideration in the structural analysis, the constitutive relations for an unsymmetrically и-layered laminated composite plate (к=1,2,..и), and without transverse shear deformations can, after integration through each ply thickness and summation, be written in matrix form as:
 (14a)
(14a)
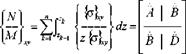 |
Or in compacted matrix form:
where N and M are the resultant in-plane forces and bending/ torsional moments, respectively. Whereas, є0 and к are the asso ciated strains and curvatures.
The eco-components of the sub-matrices Ay (extensional eco-stiffnesses), By (coupling ecostiffnesses) and Dy (bending eco-stiffnesses) are expressed as:
bending eco-stiffness matrix. Thus,
and Equation (14b) may be written as:



