The homogenization process seeks to obtain equivalent homogenous continuum properties for a medium composed of multiple phases of varying constitutive properties. For the current discussion, we will limit ourselves to a heterogeneous medium consisting of collimated, continuous fibers within an isotropic matrix. Many methods and closed-form expressions have been developed to achieve this goal (Pindera et al., 2009). Among these, the most accurate in predicting the average response of an orthotropic medium is the finite element method (Daniel & Ishai, 2006). In the finite element approach, one would like to determine the relationship between the average stress and average strain as expressed in Equation 1.
ai = Cij (sj – ajAT) (i, j = 1 – 6) (1)
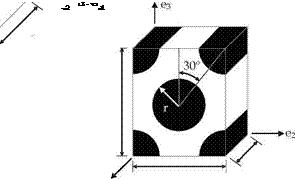
The overbar indicates an average or homogenized quantity. From the homogenous stiffness matrix (Cij), the effective lamina engineering constants (E1, E2, v12, G12, etc.) can be calculated. Alternatively, the engineering constants can be determined directly by systematically performing finite element analysis corresponding to the definitions of the engineering constants (Sun & Vaidya, 1996). In this approach, the average stress is related to the average strain through the strain energy density. Typically, a representative volume element, as shown in Figure 1, is used to simplify the analysis. Equation 2 gives the stress – strain relation for the case when AT = 0.
a = QjSj (i, j =1 – 6) (2)
Where "1" coincides with the fiber direction, "2" is transverse to the fiber direction and "3" is normal to the 1 and 2 directions. Also, note the use of a contracted notation such that i=1- 3 are the three normal components of stress and strain, 11, 22, and 33, respectively, while i=4-6 are the three engineering shear components, 23, 13 and 12, respectively. The average stress is shown in Equation 3 for the case when a canonical state of deformation is applied so that the only active strain component is s1. The superscript indicates the isolated average mechanical strain component. As shown, the relationship of can be rearranged to determine the first column of the homogenous stiffness matrix.
) = Cks1 or Ch = a(l(i = 1 – 6) (3)
The other five columns of the effective homogenous stiffness matrix are determined by applying the remaining five other states of canonical deformation such that each strain component is isolated. A total of six finite element analyses are required to fully determine the effective homogenous stiffness matrix for the general anisotropic solid. A seventh finite element analysis is required to determine the thermal response of the effective medium. For this case, the domain is subjected to a thermal loading of AT with the average mechanical strain, {s – aAT}, constrained to be zero. Equation 4 gives the calculation of the average coefficients of thermal expansion. As seen from Equation 1, constraining the average mechanical strain to be zero requires that the average stress be zero. This condition can be used to check the validity of the boundary conditions.
{ai } = sjAT (i = 1 – 6) (4)
Equation 5 shows the average strain in a unit cell determined from the surface displacement, Ui and uj with i, j = 1-3, by using Gauss’ theorem and written in index notation (Sun & Vaidya, 1996).
Where S is the boundary surface of the representative volume element and ni is the unit surface normal in the ith direction. Thus, the average strain in the unit cell can be calculated for a set of displacement boundary conditions.
Specifying the components of deformation on the surface of the representative volume element will, in general, induce average stress components. The average stress is calculated in Equation 6 using the reaction forces obtained on the boundaries of the unit cell and the definition of stress.
a,, = Fjni/A (i, j =1 – 3) (6)
 |
 |
|
Where index notation is used with Fj the jth component of the total force applied to a face with a total area of A oriented in the ith direction. In this way, all six components of the stress tensor that may result for a state of deformation applied to the representative volume element are determined.
Fig. 1. Schematics of the square and hexagonal representative volume elements (Buchanan et al., 2009)


