 |
 |
Investigating the orientation of fibers in matrix will provide both theoretical explanations for the reinforcing mechanism of short fibers and the basis for prediction and optimization of mechanical properties of NASC.
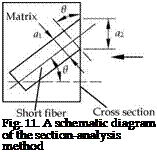
A proprietary technology was developed to obtain the fiber orientation in matrix. Four steps are involved. Firstly, cut a rectangular block of material and hold it in position by a clamp in the slicer. Secondly, slice the cross section of the material block at -423 K using the slicer
knife to machine a smooth end face, of which the normal direction should be along the rolling direction. Thirdly, visually observe the end face using a microscope associated with a high-resolution digital camera. Finally, analyze the photos and find out the configuration of the elliptical cross section of fibers. The orientation angle can be determined from the long axis and the short axis of the ellipse, as illustrated in Fig. 11.
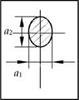
The normal direction of the cross section is in accordance with the reference direction, and the orientation angle в is the separation angle between the axial direction of a fiber and the reference direction. The relationship among в and the long axis length й1 and the short axis length a2 is in the form
в = arccos (a1 / a2) (10)
The orientation of a fiber can be characterized by a histogram, a distribution function or modified coefficients. The orientation expressed by an exponential density function f(d) is
f (O) = ^exp (-XB’)j 1 – exp (-пТ/2) (11)
where § is the fiber orientation parameter. In order to utilize the results of the fiber orientation characterization to predict the macro mechanical properties of NASC, the modified coefficients are introduced. The longitudinal modified coefficient fm. can be calculated by Eq. (12) based on the distribution function.
П
fo1= J7 f (O)cos2OdO (12)
fei is employed to evaluate the influence of fiber orientations on longitudinal mechanical property. The transversal mechanical property is evaluated by the transverse orientation coefficient fe2 which can also be obtained based on a distribution function or a histogram given by Eqs. (13) and (14), respectively.
|
П
|


