The proposed above theory predicts the behavior of composites containing nearly spherical inclusions. However, composites filled with magnetic needles or flakes are of great practical interest due to the possibility of achieving much higher permeability than the composites containing crumb-like particles with the same inclusion filling factor. A scanning electron microscope (SEM) picture for a powder with iron-type flakes is shown in Fig. 7.
Also, magnetic needles or flakes are favorable for the design of thin sheet materials. The formulation proposed herein is based on the Modified Bruggeman Asymmetric Rule (MBAR), which in terms of permeability is written as (Bruggeman, 1935)
1
= (1_ J^-t. (20)
Mi – Mhost Mhost )
 |
|
However, demagnetization factors in this formulation are missing. At the same time, it is known that the Polder-van Santen (PVS) formula, which is a consequence of the Bruggeman effective medium theory, or BSR, may account for shape factors (пк, к = 1,2,3) of ellipsoidal inclusions (Polder & van Santen, 1946),
Fig. 7. SEM picture of the magnetic powder
A flake with the disk-like shape, whose aspect ratio is и = d/h, where d is the diameter and h is the height of the disk, can be approximated as an oblate spheroid with the axial form factor being approximately (Landau & Lifshitz, 1960)
![]() 1
1
while the other two depolarization factors are assumed to be equal, nl=n2 = 0.5(1 — n3) . For high inclusion-host permeability contrast ‘fthost » 10, and for volume loading of
inclusions greater than ~30%, the resultant pf, calculated using (21), is significantly higher than the values predicted by (20), especially for the low-frequency region. This happens even for an aspect ratio of inclusions close to 1 and the corresponding form factors close to 1/3, as in the spherical case. The reason is the high-frequency nature of the BSR, analogous to the LLL, and not taking into account form factors in the BAR.
The objective is to modify the BAR for permeability (20) in such a way that it would be possible to apply it to flakes. It is appealing to retrieve the correction factor which depends
on both concentration p and aspect ratio и of inclusions from (21), as a coefficient of proportionality between spherical inclusions and flakes as
(p, u) = F(p, u)-A™ (u). (23)
and then apply the same correction coefficient F(p, u) to (20) as
MBfA (p, u) = F (р, и)-м£, (u). (24)
Effective permeability curves as functions of the aspect ratio и for varying
inclusion concentration p are shown in Fig. 8. These curves are calculated for magnetic inclusions with intrinsic static permeability of inclusions = 630.
|
40 50 60 Aspect Ratio u |
|
20 |
|
30 |
|
70 |
|
80 |
|
90 |
Fig. 8. Effective permeability calculated using BSR (EMT – effective medium theory) and corresponding curve-fitting to retrieve the function (p, u)
The closed-form expression for the correction factor F(p, u) is obtained by analyzing numerous dependencies as those in Fig. 8, and can be well approximated by the function
F ( u) =1 + {G – tanh2 (u)(1 – H – sech2(u)) / VpL ( p)}, (25)
where G and H are the fitting parameters.
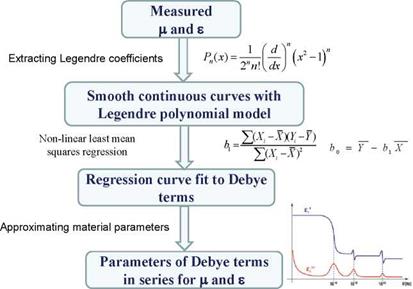
Fig. 9 shows the effective permeability of the mixture calculated using the modified BAR when the static permeability of inclusions is = 630, the resonance frequency in the magnetic Debye curve fres = 880 MHz, and p = 0.25. As aspect ratio of the plate lets increases, static permeability increases, and the loss peak shifts slightly to lower frequencies. Fig. 10 shows an example of reconstruction of experimentally obtained and curve-fitted with a sum of Debye terms (this curve-fitting will be discussed in the next Section) permeability and permittivity data for a composite containing magnetic alloy flakes with an average aspect ratio u = 25, volume fraction p = 0.5, 4nMs=4000 G, цSc =2100, and the crush
parameter 7 = ■ = 10“3. The frequency characteristic of the permeability, modeled
(d)graiu
using the MBAR, is approximated by the skewed Cole-Davidson dependence with exponents s=1.01 and £=0.6 as
y = 1 + Уы6с 1 . (26)
(l +(Jmrf)
rather than a single-term Debye dielectric curve. The simmilar formula is used for the permittivity,
It is important to mention that lus£a£ic in (26) is different from yStuk. Astatic is for the crushed magnetic material,
Relative permeability: modified BAR rule, p=0.25
When modeling permittivity using the PVS equation (21), the conductivity of inclusions is = 104 S/m; the parameters of the silicon-based polymer are taken as Static = 3.32, £host _ 2.82, and oh0St = 5.5 • 10“4 S/m. Cole-Davidson dependence exponents are s=1.01 and £=0.6. This input data gives the closest approximation to the measured results.
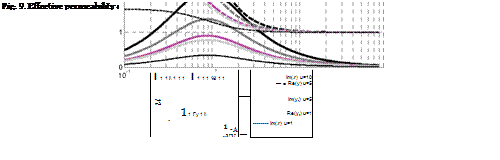
Another example is the reconstruction of the complex permeability function for two given volume loadings of flake-like magnetic alloy inclusions (15% and 25%), and prediction of frequency behavior of a composite with 30% volume fraction of the same inclusions. The results are shown in Fig. 11. In this case, the aspect ratio of flakes is u=110, 4nMs=9179 G, ^static=2000, and the crush parameter f = 10“3. The Cole-Davidson exponents are s=1.01 and £=0.65.
The proposed modified Bruggeman asymmetric rule allows for realistic predicting the frequency behavior of composites, if intrinsic constitutive parameters of inclusion and host
materials, their volume fractions, and morphology of the composite (shape and size of inclusions, their orientation, including statistical distribution of orientations, homogeneity and formation of clusters, etc.) are known a priori.
3. Material extraction procedure and curve-fitting for numerical modelling
A procedure for extracting complex permittivity and permeability of materials from measurements based on a travelling-wave transmission-line technique (single-ended and differential microstrip and stripline) has been applied. It includes an accurate and efficient
curve-fitting for approximating frequency dependencies of both permittivity and permeability by a series of rational-fractional functions. RF and microwave material frequency characteristics in the majority of cases can be accurately approximated by a series of non-resonance Debye and resonant Lorentzian terms, which have poles of the first and the second order, respectively, as
N v M X m2 r
e(m) = e + Y—^——— + Y ————————- j , (29)
ТТ!1 + jmTA 7=1m – nvi+ jm&mei meo
N x M X n2
ju(m) = 1 + У—— + Y—2————————– . (30)
ti 1 + jnTmk 7=1 m – m, + jn&nmt
The last term in equation (29) allows for taking into account the d. c. (ohmic) conductivity. The curve-fitting procedure employs Legendre polynomials and regression analysis. The flowchart of this curve-fitting procedure is shown in Fig. 12. The measured data is interpolated to smooth curves using Legendre polynomials. Then a non-linear least-mean – square regression optimization procedure is used to approximate these curves to the series
(25) and (26). For ц(а) and e(a), only Debye terms are sufficient to realize the curves, as is shown herein.
|
Fig. 12. Flowchart of the curve-fitting procedure |
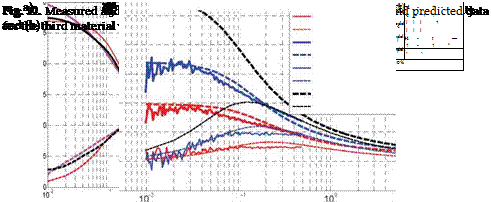
It is important that the curve-fitting procedure ensures satisfying the Kramers-Kronig causality relations, which is necessary for using these characteristics in further numerical and analytical modeling. Moreover, the proposed curve-fitting allows for restoration of the missing measurement data in some frequency intervals. For example, Fig. 10 shows the curve-fitted frequency dependences along with the measured permittivity and permeability
of the test composite material. The curve-fitting algorithm based on the Legendre polynomials and non-linear regression optimization is friendly and converges rapidly. Curve-fitting corrects non-causality of the measured responses. However, as all optimization procedures, it needs some initial guess about the Debye data to start search for the actual Debye parameters, fitting the continuous functions. These continuous functions are obtained from the series of interpolating the measured data at the discrete frequency points and smoothening using the series of the Legendre polynomials.
The curve-fitted frequency dependences of permittivity and permeability are convenient for time-domain electromagnetic numerical simulations, in particular, finite-difference time – domain method (FDTD). The advantage of time-domain techniques is that they efficiently provide broadband responses of the modeled structures. FDTD code can be used for wideband simulations of complex geometries containing frequency-dispersive materials, including a subcellular feature for modeling thin layers of absorbing materials. Both bulk cells and thin-layer sub-cells in this algorithm can include curve-fitted frequency characteristics for both permittivity and permeability.
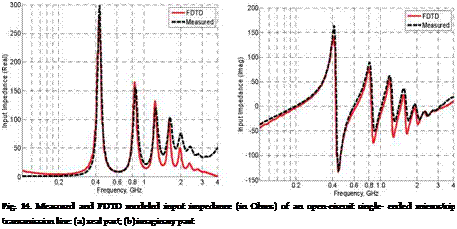
The numerical simulations have been experimentally tested for a number of structures, such as a single-ended microstrip line, a differential microstrip line, a monopole antenna comprised of a cable driven against a ground plane, and a rectangular cavity. An example with the microstrip line covered with the test absorbing sheet is presented herein. The experimental and the FDTD model setups are shown in Fig. 13. Measured and FDTD modeled amplitude and phase of the input impedance of the open-circuited microstrip line covered with a thin sheet of absorbing material with the modeled frequency characteristics as shown in Fig. 10, is presented in Fig. 14. Good agreement with experiment validates the modeling approach.
 |
Parameters of the structure
• Trace width is 3.5 mm. FR-4-type dielectric (sr=3.53; tan5=0.001), height = 1 mm.
• Characteristic impedance = 50 Q. Absorbing sheet: 10 mm x 10 mm x 0.5 mm.
Fig. 13. Single-ended microstrip line on a printed circuit board coated with an absorbing composite layer. The thick top overlay material with er « 1 is used for pressing the aborbing sheet flat
![]()
I») (b)
4.
 |
Conclusion
A methodology for engineering of new materials with desirable frequency characteristics and other physical, mechanical, and environmental properties, and their analytical and numerical modeling and experimental testing in different practical scenarios is presented in this work. The proposed methodology may be applied to design absorbers that would mitigate radiation from heatsinks, spurious radiation from chips and other active circuit components, suppress parasitic resonances within enclosures, and reduce radiation from cable structures. It is an effective approach for evaluating whether a material could be a successful candidate for mitigating unwanted radiation and coupling, and to optimize dielectric and magnetic properties of materials and their ingredients in composites, as well as geometries for particular practical problems.
5. Acknowledgment
M. Koledintseva and J. Drewniak would like to acknowledge the support of the research by the Missouri S&T Center for Electromagnetic Compatibility (U. S. NSF grant No. 0855878), and by Laird Technologies and ARC Technologies. The authors are also grateful to Mrs. Clarissa Wisner and Dr. Elizabeth Kulp (Materials Research Center of Missouri S&T) for SEM analysis of samples. K. Rozanov acknowledges the support of the study from the Russian Foundation for Basic Research (RFBR), grant No. 09-08-00158. He also is grateful to Prof. E. P. Yelsukov for providing the iron powders.