Solution of the optimization task of the curing process of composite products is as follows: necessary to find the temperature-time cycle U, which is a control parameter
U(f;f), U(f;Q*), U(f;a) = {T>(f), 71(f)}, j = 1,2,…,к*, (11)
that delivers minimum for one of the optimality criteria I and provides a high quality finished product:
– with a minimum possible duration of curing ff:
ff
If = min f dx, (12)
f U(f;ff )j V ‘
– with minimal power consumption Q*:
ff
I = minf Ta (x) dx, (13)
Q U(f;Q )0
–
or with minimal residual stresses a :
in solving the equations of the mathematical model (1)-(10) or mathematical models (Wu & Joseph, 1990), (Dmitriev & Shapovalov, 2001), corresponding to the current technique of forming products
as well as restrictions in the form of inequalities imposed on process
taking into account the allowable for equipment temperature-time cycles
* j) * Uma^b j = 1, 2,•••, ^ , (17)
where p(P) – weighting function that determines the dependence of residual stresses a of the temperature gradient (chosen empirically); Ta – working temperature autoclave, K; Tmax – maximum allowable temperature inside the material during the curing product, K; X – maximum allowable temperature gradient during curing that does not cause the accumulation of domestic stresses the material, K/m; 9 – the maximum allowable
temperature difference on the thickness of the product that does not cause the heterogeneity of the curing material, °C; Uj (t), Uj (t) – upper and lower limits of rate of heating the surface of the product at the j-th step, defined on the basis of the appropriateness of reference of the curing process, favorable conditions for the formation of curing resin structure and parameters of equipment.
Seeking a temperature-time cycle is calculated as
where K – heating rate of surface product, K/ s; kst – number of steps heating; T – temperature of isothermal hold on the j-th step of heating, K; tn – moment of transition from the stage of linear heating to the isothermal hold T, s.
A condition for the finish of the j-th step of heating and the transition to a j+1 step are:
A condition for the finish of solving the problem (11)-(19) is to achieve a given degree of cure of Py throughout the thickness of the product:
min P(x, t) >p, . (20)
0<x<L *
t0 <t<tf
Conditions (19) associated with the requirement of intensive curing process, so if the speed of curing decreased on the value of ц. and maximum temperature on the thickness of the product reduced on the value of Aj, then execute the transition to j +1 step of heating and isothermal hold. Compliance with (20) guarantees the attainment by all points of the product specified value degree of finality to the process of curing Py.
The main criterion for the quality of the finished product is its solidity, the lack of delaminating and buckling. Developing common criteria for monolithic reinforced composites is associated with large experimental difficulties and the lack of reliable experimental data on the study of strength and deformation properties of composites at elevated temperatures, especially in the curing process. Usually the monolithic criterion is given in the form of an inequality, which limits the residual and thermal stresses within the
transverse compressive strength and stretching. However, such an assignment criterion of quality products also requires a simulation of the stress-strain state of curing composite and, hence, the definition of a large number of temperature – and conversion – dependent anisotropic mechanical properties such as modules of the elastic, Poisson’s coefficients, modules of shear, coefficients of thermal expansion, etc. Therefore, the criterion of the quality of the finished product useful to associate with a temperature-conversion parameters of cure and values of the restrictions (16), which define the relationship with the mechanical properties of the composite, to determine experimentally.
From an examination of the physical essence of the physico-chemical transformations implies that the curing process should be limited to a maximum temperature Tmax, which are beginning to take place in connection undesirable side reactions associated with the destruction of resin, resulting in deteriorating the mechanical properties of cured products. This temperature is determined by the chemical composition of resin and this Tmax has a certain value for each resin.
In the curing process is usually part of the evolved exothermic reaction heat is transferred into the environment, so when curing product in it there is a temperature gradient in the direction of the cooling surface. The appearance of the temperature-conversion irregularities in the product leads to residual stresses that exceed the limit of long-term strength of the material, resulting in possible cracks, delaminating and violation of a monolithic product. For practical purposes, a comprehensive description of the inhomogeneity of the temperature-conversion field is a temperature gradient, which is directly related to the gradient of the degree of completion of the curing process.
Effects of temperature gradients in the physical and mechanical properties that arise in the curing on the thickness of the material studied with the help of special experiments, consisting in testing the mechanical properties of thin samples cured in the CMS in the context of an artificially-created temperature gradients. Setting limits damaging stresses in the bending was set temperature gradient %, which for fiberglass and carbon are in the 0,2-1 K/ mm.
In the curing of thick-walled products, one of the most undesirable modes is the curing in conditions of the front exothermic reaction because it is the most favorable conditions for the formation of residual stresses. To prevent the spread of the reaction front with the optimization process of cure can be limiting the maximum temperature difference on the thickness of the product. In addition, the large difference of temperatures on the thickness of the product contribute to the formation of various structures on the segments of the material and increase the residual stress. Limit values for the temperature difference on the thickness of products 9 for fiberglass plastics and carbon plastics derived from the testing of mechanical properties specially cured specimen is 5 ~ 8 ° C.
The choice of optimality criterion is the most subtle and responsible step in solving the problem of optimization. Based on the needs of the production of large thick-walled products made of thermosetting polymer composites, there are three main areas in the selection objective. The first – the creation of the finished products meet certain quality criteria for the minimum possible time. The second trend – the creation of high-quality finished product with minimal power consumption. Finally, the third area concerns the creation of structures products free of residual stresses, or with minimal residual stresses in a balanced state. Depending on the purposes of this decision is selected the corresponding optimality criterion (12), (13) or (14). If necessary, can be solved also the multi-criteria task of search for optimal curing cycle.
![]()
From the chemical and technological considerations the most reasonable are step curing cycles. Therefore, we can assume that in our case, the kind of a required temperature-time cycle (18) is already set, it is necessary to find only optimum speeds of heating of a product surfaces Kj on everyone j=1,2,…,k steps, the temperature of isothermal holds Tj, their durations tj and the number of steps heating kst. As a result of solution of the optimization problem defines the optimal boundary temperature-time cycles of the curing product of composites, in which the curing time tf or energy Q* or the residual stress a will be minimal. Meeting the challenge of finding the best treatment based on an incremental optimization of each of the j-th step of heating. For the optimization of the curing cycles of composite material products promising to use the penalty function method in conjunction with the algorithm of sequential quadratic programming, which is the core system software.
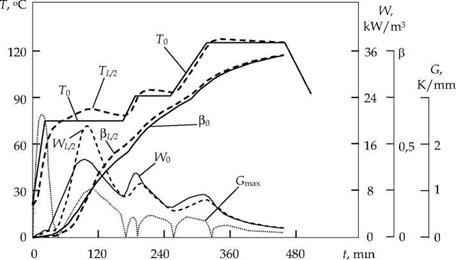
On the basis of studying the characteristics of fiberglass plastic by the developed CMS, we calculated the optimal curing cycles flat products of thickness 10 and 30 mm. The calculated optimal curing cycles plates shown in Fig. 6-7, and Table. 2.
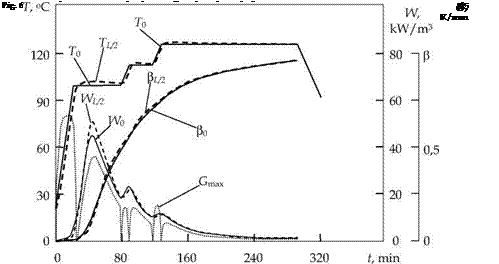
The calculations of the optimal curing cycles performed with the following restrictions: in the first step of heating the allowable on thickness the temperature gradient is G = 1 K/ mm and permissible overheating of the inner layers of AT = 8 °C, in the second and third steps of heating allowable the temperature gradient is G = 0,4 K/mm and the permissible overheating of the inner layers of AT = 5 °C (see Fig. 6-7 and Table 2). Increased temperature gradient in the first step of heating caused by reason of reducing the duration of the first hold, because degree of cure is not reached the point of gelation and the unevenness of the temperature-conversion field does not affect the accumulation of residual stresses.
optimization exceeds the specified value, then the temperature of the first hold is not selected, but rigidly defined, and its minimum duration is determined by the time required for evaporation of the solvent.
As a result of calculations, the obtained curing cycles differ from the standard cycle of smaller drops in temperature over the thickness, much smaller temperature gradients and gradual increase in the degree of curing.
|
|
|
Fig. 7. Optimal temperature cycle of curing fiberglass plastic thickness L = 30 mm
|
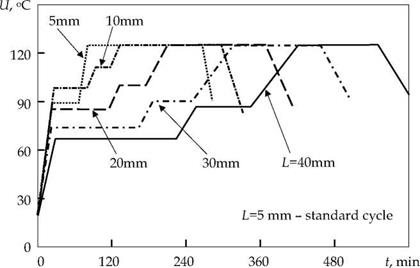
For comparison, Fig. 8 shows the existing standard cycle for L = 5 mm, and calculated the optimal cycles for L = 10, 20, 30 and 40 mm. As can be seen from the graphs (Fig. 6-8), at the increase in thickness of the product duration of curing process significantly increases and the temperature of the first and subsequent isothermal holding markedly decreased, while the evolved heat of cure reaction in the early stages of the process also reduced. This reduces the heterogeneity of the temperature and conversion fields to the specified levels %, 9 and leads to qualitative improvements of products. Due to reduction of the isothermal holding temperature levels and increase their duration reduced the intensity of the process, and the total duration of isothermal holding for thick-walled products increases. With increasing thickness of the product increases the number of steps heating kst, which is associated with the desire of optimization algorithm to intensify the curing process while satisfying the restrictions (16). These curing cycles are optimal in terms of strength characteristics and minimal residual stress, ensure high quality and low cost products due to the minimum duration and power consumption. They had no sudden changes in temperature and degree of cure in thickness, which contributes to the formation of relaxed homogeneous structure of the composite.
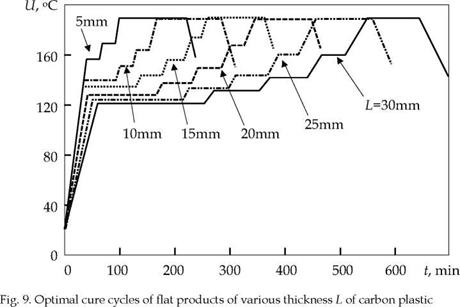
Similar properties have been studied and calculated the optimal curing cycles flat products in thicknesses from 5 to 50 mm made of several types of materials such as fiberglass plastics, organic plastics, carbon fiber reinforced plastics and rubbers. As an example, Fig. 9 also shows the temperature-time cycles of curing carbon fiber reinforced plastic thickness to 30 mm.
|
Fig. 8. Optimal cure cycles of flat products of various thickness L of fiberglass plastic |
The criterion for the end of the curing process is to achieve of dielectric permittivity to ended maximum allowable values and stabilize the dielectric loss.
The analysis and comparison of the calculated curing cycles flat products made of composites with existing cycles designed for thin products demonstrated the feasibility of widespread use of the method of mathematical modeling and optimization for testing of existing and calculation of the curing cycles of new composite materials, as well as the further development of the method.
|
|
3. Conclusion
Presented an example of determining the optimal curing cycles of plates of different thickness of the composites based on thermosetting resins demonstrates the need to implement in practice when determining the curing cycles of the method of mathematical simulation and optimization. The method allows to repeatedly under different conditions to simulate the curing process on the computer, that is calculate the temperature-conversion field during curing of composites, as well as represent them in the form of graphs and 3D surfaces, thereby analyze uneven curing and quickly assess the advantages and disadvantages of the curing cycle for the material and choose the correct strategy for optimizing the production cycle, thus obtain high quality finished products with minimal energy consumption, or with minimal residual stresses.