Solutions in the nonlinear range

The assumption introduced in the subsection 2.2 for simplifying the general eighth-order equation formulated in subsection 2.1 can be generally assumed as a reasonable trade-off between the (good) accuracy of the obtained model and the (higher) simplicity of its equations. The approximation introduced by the supplementary assumption is generally accepted especially in the nonlinear range, as further uncertainties are introduced by the fracture behaviour of concrete which cannot be covered by the complex assumptions leading to equation (32).

Thus, the nonlinear response of FRP-to-concrete joints under pull-out actions can be analyzed by assuming the problem described by equation (42) with the boundary conditions in (44). Since the nonlinear response is now of interest, equation (42) can be slightly modified for considering the possibility of a nonlinear relationship Ta=i(s). Moreover, eq. (1) can be written in terms of axial strains є in the FRP strip by introducing equation (8):

— + Ef = 0 . (45)

dz Eftf

and, considering the relationship between axial strains and interface slip derived at the end of the subsection 2.2, the following relationship can be written for generalizing eq. (42) to the nonlinear range:

. 0

dz2 Eftf

The bilinear shear-stress-interface-slip relationship is considered herein as a general relationship for the nonlinear response of the interface between FRP and concrete:

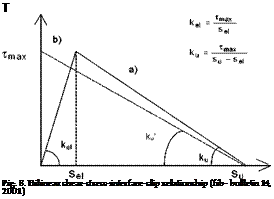
where all symbols are represented in Fig. 8. For the sake of simplicity, only the monotonic behaviour with s>0 will be considered in the following elaborations.

Consequently, two second order differential equations can be obtained by introducing the two nonzero branches of the relationship (47) within the general equation (46). In particular, under low load levels, the condition 0<s<sel yields throughout all the bonding length and the equation (46) can be written in the following form in terms of interface slips s:

-и2.s = 0 . (48)

dz2

Considering a pull-out force P applied at the end (z=L) of the bonding length, the following boundary conditions can be written after eq. (44):

Simple mathematical transformations (whose details are omitted herein) lead to the following solution in terms of interface shear stresses

which can be easily turned in terms of interface slips s considering the expression describing the linear elastic branch in eq. (47). This solution can be accepted for values of the shear strength |T < Tmax or, in order words, for pull-out forces lower than Pel:

Fel = Tmax • bf. (51)

ю

leading to an interface slip s=sel in z=L. As P>Pel, two different parts of the adhesive interface can be recognized. In the first part, namely for 0<z<zel<L, the values of the interface slips s keep smaller than the elastic threshold sel. In the second part, for zel<z<L, the interface slips s are in the range (sel, su), and the following solution can be derived by integrating the two differential equations:

(52) (53) (54) (55)
ds1 dz	ds2 dz
sd = sJ 1|z = zel ilz = zel

The following solution in terms of interface shear stress т involves the parameter zel<L, describing the length of the elastic part of the bonding length:

cosh(ю • z T ———————————— — max і / cosh(co-zel) 0 < z < zel (56) zel )]-— •sin к (z – ю zel )^- tanh (cozel) ■ zel < z < L ю hmax/ (su sel) in У Eftf (ki^ v Eftf ‘ (57)

T

where

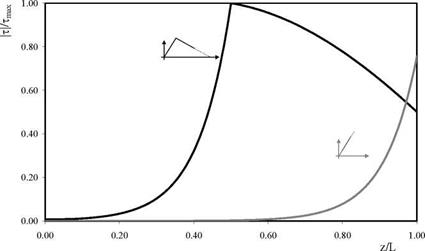
Fig. 9 shows two typical distributions of shear stresses in the a) linear and b) nonlinear range of the behaviour of the adhesive interface described by the bilinear relationship in eq. (47).

It is worth noting that zel can actually range in the interval [zel, min, L):

el, min = max {0;zel, deb}

in which zel, deb is the value of zel leading to t(L)=0 (or s(L)=sJ:

cos [rota (L – zeldeb)]	– Zel, deb )]’ tanh Zel, deb )= 0-
(59)
Fig. 9. Typical distribution of interface shear-strength in the linear and nonlinear range 2.4 Key parameters related to the ultimate strength The case of zel, deb=0 is of particular relevance, as it represents the condition of debonding initiation (namely, s(L)=su) with T(0)=Tmax. A characteristic length Leff can be defined in that case by means of equation (59):

(60)

Under the mechanical standpoint, this characteristic value has a paramount conceptual meaning. It represents the border between "short" and "long" anchorage length. In particular, the general expression of the force F>Fel corresponding to a given position of zel can be derived by integrating the shear stresses in equation (56):

It can be applied if and only if zel є [zel, mm, L) (namely, the interface slip s is sel <s<su). In the case of zel=L equation (61) reduces to (51). On the contrary, when zel=zel, deb=0 the following expression can be derived for the pull-out force:

Since generally su>>se the value Fdeb is only slightly lower than the maximum strength Fmax which can be evaluated by applying the theory of Fracture Mechanics (Taljsten, 1996) (or either as a maximum on zel of the for F in eq. (61)):

Fmax = bf Л/2GF • Eftf = bf. (63)

They can be assumed as coincident in the approximation of rigid-softening behaviour in considered Fig. 9.

Note that equation (63) can be applied only if Lb > Leff being Leff, the effective transfer length. If Lb < Leff a smaller value of the ultimate force has to be expected according to the following relationship:

(64)