Dynamic loading of the composite panels is provided by a SHPB for compression tests. The longitudinal impact load F0 of the striker generates the uniaxial stress pulse transmitted to the input bar as:
a(t)= S = (pp)Vp () (1)
S
c0 is the velocity of the wave pulse, bars of Sb is the bars cross-section area, Vp (t) the particle velocity, and p the density of the striker material. Accurate measurements of the wave pulse and particle velocity in dynamic impact studies are important since the wave pulse is in fact the propagation of the disturbance or vibration of the particles. The amplitude of the incident wave pulse depends on the impact velocity (a function of the applied air pressure) and material properties of the striker.
d2u d2u n —t – c0 —t = 0
dt2 dz2
C0 =<E7 p, E0 is the Young modulus and u(z, f) the longitudinal displacement. The solution yields:
du a du. .
dz c0 dt
a = -1 for wave propagation in the positive direction, a = 1 for the wave propagation in the negative direction. It leads to solutions: u = u (z – c0t) for a = -1 and u = u (z + c0t) for a = 1.
The particle velocity is as follow:
du (z, t)
dT~
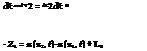Velocities with the interfaces specimen/bars are: V1 = dZy where Z1 = z1 + u (z1,t) and Z2 = z2 + u (z2, t)
With the deformation, the length of the specimen is L = Z2 where L0 = z2 – z1. Then:
L = L0 -_[( – V)dt (5)
0
Equations (6) and (7) give respectively, the strain, the stress and the strain rate in the sample. ei, er, et being respectively the incidental and reflected deformations pulse at the input bar/specimen interface and that transmitted by the interface specimen/output bar interface, Figure 1b. Those are determined by transport formulas of the signals of the gauges towards the interfaces specimen/bars. This transport takes into account the correction of the dispersive character of the propagation, of the deformations pulse in the bars, by optimization of the decomposition coefficients, in series of Fourier, of the signals. The particles in the input bar will propagate to the right at a relative velocity of Vb in the longitudinal direction of the wave pulse. With a specimen of cross-sectional area S0 ,
sandwiched between the input and output bars, equilibrium at the interfaces is satisfied by the continuities of forces and velocities at the interfaces such that the particle velocities, sample stress, strain and strain rate for a thin sample are derived as:
V =-C, h
Vr = c0 t Vs =-c0 [t + t-h ] = -2c0h
Vt =-c0 h
Assuming equilibrium in short specimen, tt = ti +tr; the strain, strain rate and stress is:
2 c t
h =- T° h (t )dt
T0 0
d =- T0 t () (7)
(t)
C0
