The hetrojunction layers compounds in solar photovoltaic cells: CuInSe2, CuInS2, AgGaSe2, and AgGaS2

Various attempts have been made to correlate the bulk modulus of compound semiconductors and chalcopyrite compounds with many other physical parameters. Nevertheless, it is found that bulk modulus interconnected well with strength and hardness in many materials (Choi & Yu, 1996). Therefore, the material stiffness and its corresponding bulk modulus is one of the important factors that characterize the physical property of a material system which quantifies the degree of stiffness or the energy required to produce a given volume deformation. With a good agreement result, an empirical expression for the bulk modulus was obtained by Cohen (Cohen, 1985) based on the nearest-neighbour distance. Using the total energy method Lam et al. (Lam et al., 1987) obtained an expression for bulk modulus with acceptable results. The bulk modulus for the semiconductor compounds was found to be inverse proportionally correlated to the lattice constants (Lam et al., 1987 & Al-Douri, 2004). Gaith et al (Gaith & Alhayek, 2009) have studied the correlation between the bulk modulus and the over all stiffness and lattice constants for CdX and ZnX (X=S, Se, and Te) using orthonormal decomposition method (ODM) (Gaith & Alhayek, 2009) from continuum mechanics point of view.

The purpose of this section is to understand how qualitative ground state concepts of the hetrojunction layer compounds, CuInSe2, CuInS2, AgGaSe2, and AgGaS2, such as overall elastic stiffness, can be related to bulk modulus and lattice constants. Therefore, using the elastic coefficients for anisotropic material, an elastic stiffness scale for such anisotropic material, and a scale to quantify the isotropic elasticity within the material will be discussed. The number of elements of the decomposed stiffness tensor should be equal to the number of non-vanishing distinct stiffness coefficients, i. e., six constants for tetragonal materials, that can completely describe the elastic stiffness in that medium. Thus, using Orthonormal Decomposition Method (ODM), namely, Orthonormal Tensor Basis Method (OTBM) (Gaith & Alhayek, 2009; Gaith & Akgoz, 2005), the matrix representation for the elastic stiffness with tetragonal symmetry system is decomposed into a contracted form as shown in Eq. (29):

C C 0 0 0 11 12 13 C C C 0 0 0 12 11 13 C C C 0 0 0 C. = 13 13 33 4 0 0 0 О u 0 0 0 0 0 C 0 44 0 0 0 0 0 C 66 4 -2 -2 0 0 0 " -3 -1 -2 4 -2 0 0 0 -1 -3 -2 -2 4 0 0 0 -1 -1 +A + A, 2 0 0 0 3 0 0 3 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 3 0 0 ■-3 -5 4 0 0 0" "-1 1 -5 -3 4 0 0 0 1 -1 4 4 0 0 0 0 0 0 +A +A 4 0 0 0 1 0 0 5 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 "-1 1 0 0 0 0" 1 -1 0 0 0 0 0 0 0 0 0 0 +A 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

(29)

where

A 1 90 (2C11 + 2C12 + C33 + 4C13)

A 2 = 45 (2C11 – C12 + 6C44 + 3C66 + C33 – 2C13) 1

A a = —(-3Cі – C „ -4C . . – 2C,, + 6Caa -2C. a 3 90 11 12 44 66 33 13

1

A 4 = 144(-6C11 – 10C12 + 8C44 + 4C66 + 16C13) 1

A ^-(-2C1+2C.+8C^-4aj 5 16 11 12 44 66′

1

A6=^(-2C11 + 2C12+4C66)

Where A і to A 6 are constants in terms of elastic stiffness coefficients expressed as in Eq.

(30). It can be observed clearly that the first two terms on the right hand side are identical to the corresponding well known two terms namely bulk and shear (Gaith & Akgoz, 2005) which are identical to those found in literature (Voigt, 1889) for the isotropic system (Hearmon, 1961). Here, A1 and A 2 defined in Eq. (2), are the Voigt average polycrystalline

bulk B and shear modulus G, respectively. Hence, it can be stated that the tetragonal system is discriminated into the sum of two parts: isotropic part (first two terms), and anisotropic part (other four terms). The latter part resembles the contribution of the anisotropy on elastic stiffness in the tetragonal system.

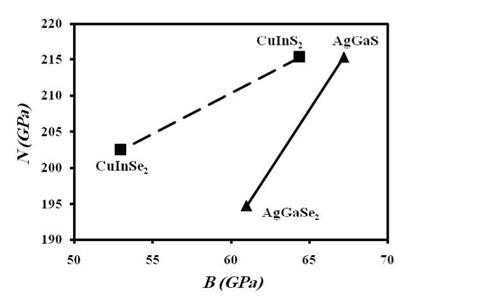
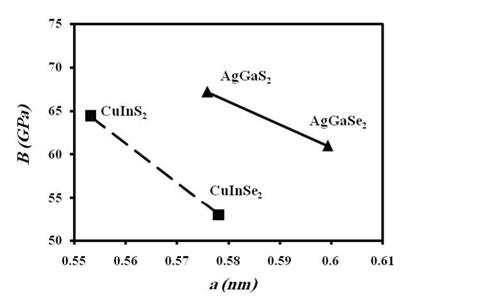
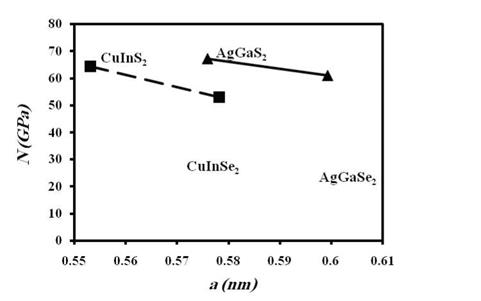
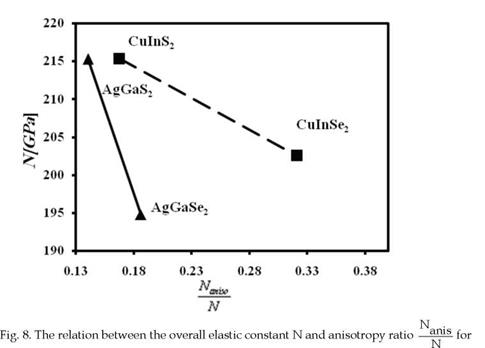
In solar energy technology, thin film solar technology based on the hetrojunction layer compounds CuInSe2, CuInS2, AgGaSe2, and AgGaS2, is very promising due to lower production costs and shorter energy pay back times (Fischeret al., 2006). For these compounds, the successful interface between absorber and buffer layers with alternative materials requires structural and optical material characterization as a prerequisite for understanding interfaces in photovoltaic devices (Fischeret al., 2006). On the other hand, stability of these compounds in solar cells is of concern due to their application in space, where the cells have to withstand high energy particles, mainly electrons and protons that can cause severe damage in solar cells up to a complete failure. Therefore, the radiation hardness and damage mechanism of the hetrojunction layer compounds solar cells is associated with the overall elastic stiffness and bulk modulus (Batzner et al., 2004). The materials elastic stiffness coefficients and lattice constants for CuInSe2, CuInS2, AgGaSe2, and AgGaS2 are presented in Table 7. The correlation trend between overall elastic stiffness N and bulk modulus B for each group, i. e. (CuInS2, CuInSe2) and (AgGaS2, AgGaSe2) is clearly shown in Fig. 4; the overall elastic stiffness increases as the calculated bulk modulus B increases. Besides, the calculated bulk moduli are in good agreement with those found by theory of anisotropy (Hearmon, 1961) and experimental values (Cohen, 1985). Also, the bulk modulus for each group is inversely proportional to lattice constants a, as shown in Fig. 5, which was confirmed in several studies (Lam et al., 1987; Al-Douri et al., 2004; (Christensen & Christensen, 1986; Al-Douri et al., 2001). Consequently, the overall elastic stiffness N is inversely proportional to lattice constants a, as shown in fig. 3. CuInS2 and AgGaS2 have larger elastic stiffness, largest bulk modulus, and lower lattice constant than those for CuInSe2 and AgGaSe2, respectively. Therefore, the overall elastic stiffness and bulk modulus, the only elastic moduli possessed by all states of matter, reveal much about interatomic bonding strength. The bulk modulus also is the most often cited elastic constant to compare interatomic bonding strength among various materials (Pantea et al., 2009), and thereafter the overall elastic stiffness can be cited as well (Gaith & Alhayek, 2009).

For the isotropic symmetry material, the elastic stiffness tensor is decomposed into two parts (Kim & Chen, 2004; Spencer, 1983; Voigt, 1889; Hearmon, 1961); meanwhile, the decomposition of the tetragonal symmetry material, from Eq. (29) is consisted of the same two isotropic decomposed parts and other four terms. The Norm Ratio Criteria (NRC) used in here is similar to that proposed in (Gaith & Alhayek, 2009; Gaith & Akgoz, 2005). For tetragonal symmetry materials, the elastic stiffness tensor has the same two parts that consisting the isotropic symmetry materials and the other four terms, will be designated as

N.

the other than isotropic or the anisotropic part. Hence, two ratios are defined as: —for N i

the isotropic parts and —for the anisotropic parts. The norm ratios can also be used to

assess the degree of anisotropy of a material property as a whole. The norms and norm ratios for the hetrojunction layer compounds CuInSe2, CuInS2, AgGaSe2, and AgGaS2 are

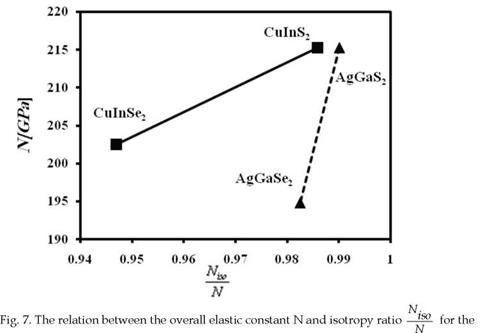
Niso

calculated and shown in Fig. 7 and 8; as the isotropic ratio —increases, the anisotropic

Nanis

ratio —anls decreases and this confirms the definitions of these two ratios, and the bulk N

modulus increases at the same time.

Niso

Therefore, CuInS2 is a closer material to isotropy (or less anisotropy), with —= 0.9859,

and larger bulk modulus B = 64.43 GPa than those for CuInSe2. Similarly, AgGaS2 possesses a closer material structure to isotropy and larger bulk modulus B than those for AgGaSe2.

	C11	C12	C44	C13	C33	C66	a
CuInS2							0.5532
(Pantea et al., 2009)	83.7	54.4	34.5	54.8	84.5	33.9	(Krustok et al., 2001)
CuInSe2							0.5782
(Pantea et al., 2009)	71.0	45.3	45.5	45.3	63.3	47.4	(Kannan et al., 2004)
AgGaS2							0.5759
(Grimsditch & Holah, 1975)	87.9	58.4	24.1	59.2	84.5	30.8	(Chahed et al., 2005)
AgGaSe2							0.5993
(Eimerl et al., 1991)	89.8	65.7	21.7	45.1	63.3	13.3	(Chahed et al., 2005)

Fig. 4. The relation between the overall elastic constant N and bulk modulus B for the hetrojunction layer compounds

Fig. 5. The relation between the bulk modulus B and lattice constant a for the hetrojunction layer compounds

Fig. 6. The relation between the overall elastic constant N and lattice constant a for the hetrojunction layer compounds

hetrojunction layer compounds

the hetrojunction layer compounds

A significant contribution of this decomposition method is the direct correlation between the macroscopic and microscopic features of a material by means of symmetry properties. Based on the Orthonormal Tensor Basis Method (OTBM), the elastic stiffness for tetragonal system materials into two parts; isotropic (two terms) and anisotropic (four parts) is presented. The overall elastic stiffness is calculated and correlated with lattice constants and calculated bulk modulus for the hetrojunction layer compounds CuInSe2, CuInS2, AgGaSe2, and AgGaS2. The overall elastic stiffness is quantified and correlated to bulk modulus and inversely proportional to lattice constants. CuInS2 and AgGaS2 have larger overall elastic stiffness and bulk modulus and the smaller lattice constant than CuInSe2 and AgGaSe2, respectively. Based on the Norm Ratio Criteria (NRC), the hetrojunction layer compounds CuInS2 and AgGaS2 are closer to isotropy (or less anisotropic) than CuInSe2 and AgGaSe2.

5. Conclusion

Any physical property is characterized by n rank tensors, and this method is capable for decomposing these tensors with intrinsic symmetry, which is derived from the nature of the physical property itself, of any rank into orthonormal tensor basis. This method is capable to decompose tensors with non-intrinsic symmetry of rank n by generating an orthonormal basis using the well Known Gram-Schmidt process for the corresponding symmetry media of that tensor, and the number of basis elements should be equal to the number of non­vanishing distinct coefficients in that media. The decomposition procedure developed in this work has many engineering applications in anisotropic elastic materials which are, both
qualitatively and quantitatively, different from isotropic materials. A new innovational decomposition of general and more explicit physical property for the symmetric second rank stress and strain tensors is introduced. The results are compared and found to be identical for special cases available in literature (Spencer, 1983; Cowin & Mehrabadi, 1987; Hue & Del Piero, 1991; Srinivasan, 1998; Blinowski & Rychlewski, 1998; Tu, 1968; Nye, 1959; Ikeda, 1990). Nevertheless, this method is introducing a new form of decomposition that has a more featured and transparent physical information. The Criteria to measure the overall effect of the material properties proposed using the norms to represent the piezoelectricity and stiffness effect in the material like piezoceramics and fiber-reinforced composites, respectively. Through this method it is possible to study the effect of angle orientation of fibers and the material properties of fiber and matrix on the stiffness of the composite. A new proposed norm ratios criterion is introduced to measure the anisotropy degree and compare it with other materials of different symmetries. These ratios can be used to study the linear and non-liner damage parameters using total energy for fiber reinforced composite structures (will be published soon).