Third rank tensors

In the continuum approach to the study of anisotropic solids it is well known that certain physical properties can be represented by tensors. The polarization of a crystal produced by an electric field is an example of an anisotropic material property that is represented by tensors. If a stress is applied to certain crystals they develop an electric moment whose magnitude is proportional to the applied stress; known as piezoelectric effect. The piezoelectric effect in materials has not attracted much attention until after the Second World War, since when the applications and the research of piezoelectric materials have advanced greatly. Piezoelectric materials nowadays have been widely used to manufacture various sensors, conductors, actuators, resonators, oscillators and monitors. They also play an important role in the so-called smart structures. In fact, piezoelectric materials have been applied extensively in electronics, laser, ultrasonics, microsonics, naval and space navigation as well as biologics and many other high-tech areas. The piezoelectric coefficients appear in the equation Pj = dijkajk, where Pj are the components of the electrical polarization vector

and ajk, the components of the stress tensor. The form invariant expressions are derived for

many classes of piezomagnatic (Srinivasan, 1970), and piezoelectric coefficients (Tsai, 1992). Although such constitutive equations are form invariant with respect to arbitrary orthogonal coordinate transformations, the coefficients, dijk, do not determine directly the

material constants since their values vary with the direction of the coordinate axes. The piezoelectric coefficients with the following symmetry dijk = dikJ the number of non­vanishing independent coefficients is reduced from 27 to 18 independent coefficients for the triclinic system. For the monoclinic system, for example, of class 2, the number of independent coefficients is reduced to 8, for the orthotropic system of class mm2 is reduced to five coefficients, and for the hexagonal system of class 6mm is reduced to three independent coefficients. The form invariant expression for the hexagonal system class 6mm is (Srinivasan, 1970)

dijk d183i83j83k +d2(83k8ij + 83j8ik) + d383i8 jk

Following the same procedure used for second rank tensor, the basis elements are

Tijk 83i83j83k

j 72 (83i8jk – 83i83j83k)

TjkI=^(83k 8ij + 83j8ik-283i83j83k)

The decomposition of d„k is given in terms of this basis elements as

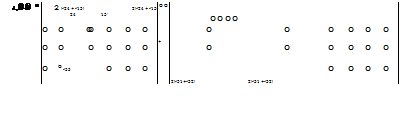where (d, Tijk) represents the inner product ofd^and qth elements, Tqk of the basis.

independent piezoelectric coefficient. If a tensile stress <r3 is applied parallel to which is a diad axis of the crystal, the first matrix in (18) shows that the components of polarization are given by the moduli in the third column of the first matrix. Thus, the decomposition that we present is decomposing the polarization along orthogonal axes into three parts; the first part is the polarization along the diad axes due to normal stress, the second part, the polarization along the nondiad orthogonal axes due to normal stress, and the third part, is the polarization due to the shear stresses.