If a multiplication component is part of a p-graph, then during the production of the i-tree the corresponding subtree is generated as many times as is indicated by the corresponding parameter of the multiplication component. Hereby all copies of the child components are connected with the copy of the multiplication component.
During production of the i-tree the component prototypes are transformed into instances. The difference between a prototype and an instance lies in the definition of most of the parameters that are passed on to the child components, such as their local coordinate system. In a component prototype these parameters are stored as ranges, while the instances in the i-tree receive fixed and individually computed values during multiplication through interpolation.
If, for example, the sizes of the children are set in the range [no, ui] in a multiplication component, then the ith child of n is assigned the value =
v0 + (i – 1)(v1 – v0)/(n — 1) with i = 1,…, n, n > 2 by interpolation. If nec-
essary, before their transmission, a user-defined function can be applied to the interpolation values. In this way trigonometric functions and/or random values can be integrated into the models.
Similar to the procedural multiplications during the production of the i-tree, recursions are treated. In each component the maximum recursion depth is defined as a parameter. If a recursive definition must be expanded, after generating an appropriate number of instances, the expansion is stopped. Referring back to the statements concerning recursive algorithms in Sect. 4.6, it is evident that this form of modeling is not required frequently.
After the i-tree has been constructed, a depth-first traversal starting at the root is performed up to the leaves. The root component generates its geometry and forces all its children to do the same. This is recursively continued, until the entire i-tree has been processed.
The following further demonstrates the process of geometry production: Let A be the component prototype of the root of the p-graph, and B be the prototype of a geometry-generating component, which produces a stem. Let C be a multiplication component, which is forced to generate three instances of the successor, but no geometry. Component prototype D generates likewise a small stem. In the example a recursion depth of three is set by the user. The graph is defined so that a recursion is defined on D.
|
|||
 |
|||
|
|||
|
|
||
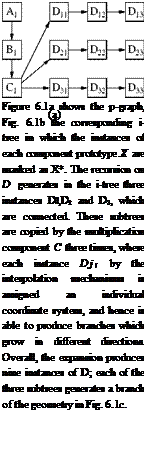6.1 Component Types
The system components can be divided into three classes: geometry production, multiplication, and global modeling. All components have a basic set of
|
|
|
|
|
