 |
 |
In raytracing, a great amount of computing time must be spent on the so-called ray query. Here, with each tracing ray, we have to check which object or polygon of the scene is hit first. On the other hand, in local illumination models a lot of work is due to the visibility calculation, which defines for all polygons of each object whether or not they are actually visible. In both cases the efforts can be simplified and the computing time decreased, if complex objects are approximated using simple bounding geometries such as cubes or spheres, which include these, so-called bounding objects or bounding boxes [108,180]. If such objects were produced, then for the ray request as well as for the computation of the visibility the bounding object can be used for a first test. Only if it was hit or if it is visible is the actual object taken into consideration. In this way a conservative assessment is reached: if the bounding object is not visible, the included geometry is also not visible. However, it is possible that the bounding object is visible, while the actual geometry is not.
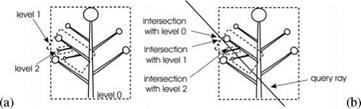
In the case of plant geometries, the approximation with bounding objects is especially meaningful, since these are very complex, and, as already mentioned, are mostly compact objects. The recursive structuring of trees and shrubs permits hereby also a recursive, nested description with bounding objects. The entire plant is embedded into an enclosing object. This contains the bounding objects of the main branches, and these again contain the bounding objects of the smaller branches, and so on. This is continued until the amount of geometry to be included is small enough so that a further approximation is not worthwhile.
At the request, first the overall bounding box is tested. If the result is positive, then the next-closest approximation is treated, and so on. This way, a request can be handed down in a cascade and decided on with a minimum of effort. Figure 9.10 shows the structure of a hierarchical approximation with bounding objects and the ray query.



