For the most part, the appearance of a natural landscape is determined by erosion, in that material is cleared away, and rough edges are sanded off. Additionally, there are many other factors that alter the form of a landscape. in computer-assisted simulations of landscapes, this can be illustrated in two different ways: Either erosion-like appearances can be produced using a local change of the fractal generation of a landscape, or erosion processes can be simulated on existing height fields using geomorphologic methods.
|
|
|
Musgrave et al. [143] extends the already discussed synthesis methods for eroded mountains by the simulation of water paths. Prusinkiewicz and Ham – mel [163] combine midpoint displacement with predefined river basins, in order to integrate rivers into their mountain models. However, the visual results are not very realistic looking. However, in his system “Mojoworld”, Musgrave included recently a physical water simulation that yields better results. Geologically oriented simulation methods generally are well suited for synthesizing such complex processes. From the view of geomorphology, the forms and shapes of mountains evolve from complex interactions between endogenous and exogenous influences, such as crustal deformations or crust movements and volcanism, and weathering, demolition, and depositing. Endogenous processes are mostly responsible for relief increase, the exogenous processes are usually relief decreasing.
There have been several attempts to replicate both processes and thus to create realistic-looking mountain ranges [146], though erosion procedures are in most cases applied to already-existing terrain. With respect to the so-called geomorphodynamic system (see [4]), processes are differentiated as follows:
■ Weathering
Weathering denotes the process that disintegrates rock at the earth’s surface due to exogenous activities. According to the kind of the modification of rock and soil material, we distinguish between mechanical disintegration and chemical decomposition. With mechanical disintegration rifts and crevices result from variations in temperature, and the rock is broken up into smaller rocks without altering their composition. Chemical decomposition causes the rock to slowly decompose, and at the same time alters its constituent minerals. on the basis of the observation that the decomposition decreases exponentially with increasing depth under the surface, the mechanical decomposition rate Wm (erosion per time) can be computed using
Wm = Wo e-klC, (7.7)
where W0 is the rate with uncovered stone, k1 is a coefficient depending on the material, and C is the height of the regolith, the already-existing weathered material such as sediment, soil, or stones [3].
In contrast to mechanical weathering, chemical weathering reaches its maximum at a depth, at which sufficient moisture is stored to still preserve chemical decomposition processes during dry periods. For regolith depths below this maximum, chemical weathering increases with increasing C.
if the regolith cover is denuded through additional erosion processes, the effect of weathering is likewise changed. in sum, we are dealing with a complex interactive system.
■ Denudation
Denudation here means the planar wearing away of the soil cover as well as the relocation and deposition of rock material. in combination with weath-
ering, and as a result of insufficient decomposition, a so-called decomposi – Section 7.3 tion-limited denudation can develop – an example is ravines – or, in the Erosion
 |
 |
reverse case, a transport-limited denudation is caused.
The form of rock slopes is affected considerably by the type of denudation: On slopes mechanical degradation first dominates and then usually a decomposition-limited denudation prevails without a visible regolith. Transport-limited denudation, however, leads to planar, continuously regolith – covered overhangs, almost like detritus [4]. The mass balance for each point of a slope is described as follows:
C = Co + (W + A – R)AT, (7.8)
where C describes the depth of the regolith at the end of the time span denoted by AT, C0 is the initial regolith depth, W is the weathering rate, A is the rate of sediment supply through denudation transport, and R is the rate of sediment discharge.
According to the kind of medium being transported, different types of denudations can be distinguished, in particular the gravity-conditioned mass movement of rock and debris which is important for the visual appearance as well as the decomposition by rain.
The modeling of debris slides depends on the types of material. specific angles are used from which material begins to slide (e. g., sand at approximately 27-33°, sand gravel at up to 50°).
The sliding process can also be modeled over a system of finite differences: a uniform grid is laid over the terrain (the grid usually corresponds to the grid for geometry production, but can also have different grid widths). At the grid nodes material is accumulated, which is then distributed to the adjacent points during the process of simulation as a function of the terrain’s
local angle. This method is a discretized solution of the system of differential equations described by Eqn. (7.8).
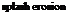
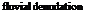The spattering of sand, silt and clay/stone particles, i. e., small soil particles, caused by the impact of raindrops on very wet soils is called splash erosion. The loosened and separated particles may or may not be subsequently removed by surface runoff. Here the parabolic flight paths of the particles on a slope surface are somewhat longer downwards than upwards, which causes the movement of the material to lower levels.
Rainwater collected on the surface flows down the slopes, whereby the water drops merge into a system of river-like branched flumes. Soil particles are carried forward with this fluvial denudation and fed into the brooks. Again the process can be described by a system of finite differences (see Musgrave [142]).
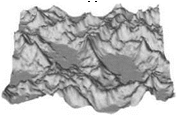
Figure 7.6 illustrates the effects of different denudation processes. The splash erosion produces a distinct abrasion effect. Through debris sliding, the maximum slope inclinations are adapted, which, however, produces no substantial effects on the illustrated terrain. The fluvial denudation deposits clearly visible material in the dips.
Erosion
By the term erosion, we mean, in contrast to the planar-working denudation, the rill and carving effect of flowing water along line-like decomposition courses. In particular, in rivers and glacier valleys, loosened rock rubble is cleared away by the friction force of the water, and through collision with other rock chunks. Erosive decreasing of the riverbed is called riverbed erosion, while the erosive displacement of river or stream banks is termed bank erosion.
Although erosion is perhaps the most important contribution to the visual modification of mountains, so far only comparatively few works have been published on this topic in computer graphics. Kelley et al. [109] modeled river valleys and networks over parameterizable tree models, which generated a fractal branching structure. According to the branching between the river courses, surfaces are stretched, and over an optimization suitable gradients are obtained.
The previously introduced works of Prusinkiewicz and Hammel [163] as well as Nagashima [146] are among the few approaches that focus on the generation of river courses in combination with the modeling of mountains. Musgrave worked with a similar model in his system of landscape generation [142]. Nevertheless, the results obtained using these methods still allow for a vast scope of development.
interestingly enough, so far no methods have been presented that consider the interaction of erosion and vegetation, at least not in computer graphics. Since even a thin plant layer decisively changes the effect of weathering and decomposition, and the corresponding modeling would produce interesting results, this area should definitely be focused on. However, the three-dimensional
forms of the objects involved play an essential role in the necessary detailed simulations, which makes the algorithms far more complex.
