If the distribution patterns are not explicitly given, but their spatial statistical characteristics are known (see Sect. 3.5), then random-number generators can be applied for their production.
This can be implemented in two ways: either points are generated one after the other and then inserted into a point set, until the given specification is reached, or a point set is changed in such a way that its statistical characteristics correspond to given values. Both procedures are outlined shortly in the following. The first procedure class is termed iterative, the second adaptive.

![]() An approximation of a Poisson distribution can be generated iteratively by a random generator, in that each coordinate is selected randomly independent from the others. The mean per region is determined by the number of points, divided by the area surface. Algorithms of this type are also called DartThrowing algorithms.
An approximation of a Poisson distribution can be generated iteratively by a random generator, in that each coordinate is selected randomly independent from the others. The mean per region is determined by the number of points, divided by the area surface. Algorithms of this type are also called DartThrowing algorithms.
Such a distribution can also be generated directly: a random process generates a radial increasing Poisson distribution at a given point density A after the following scheme [141]: we require independent and equally distributed unit vectors ei as well as independent and equally distributed numbers vi є [0, ..1]. The points pi are generated over
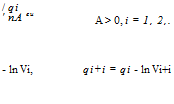
![]() where
where
The point set has then the density A and is arranged according to the increasing radius. Variations of this procedure can be used also for the production of other distributions; for example a spatial anisotropy can be modeled by a change of the unit vectors ei.
To create a Poisson disk distribution is somewhat more complicated. Due to the local characteristic of the points – no other point may be within a specified radius r around each point – direct production is difficult. Here, a variant of the dart-throwing technique can be applied.
Again points are added iteratively to the point set; now, however, the system checks whether each point to be inserted is located within a disk surrounding
one of the so far given points. If not, then the point is inserted; otherwise it is rejected. The procedure works well for distributions whose point densities are so low that the Poisson disk criterion with given r can be easily satisfied. If, however, many points are already present in the point set, the fact that only a few positions are available for other points slows down the efficiency of the algorithm rapidly.



