In Sect. 3.4 we already mentioned the remarkable effect that the mathematical method using the Golden Angle describes the arrangement of the seeds in many flowers very well, but that at the same time there is no indication of the biological emergence of these patterns. Actually, for the correct positioning of the seeds in correlation with the Golden Angle, an angle precision would be necessary that could never be reached by means of biological mechanisms.
Tests in computational biology indicate that phyllotactic patterns are the result of local optimization processes, which arrange during the growth successively developed sperm cells in an appropriate way. Growth takes place in the meris – tem, the conical point at the shoot, which contains fast-dividing cells. The produced cells are shifted by the linear growth of the branch to the outer border and there arrange themselves (see Fig. 4.17). The problem of the Golden Section is transferred here, in contrast to the flat disk, to a cylinder requiring new solutions. Thus, besides the divergence angle of the sequentially following objects, also the heights of the objects on the cylinder surface must be computed. Prusinkiewicz and Lindenmayer [166] describe in detail different approaches for such a simulation.
|
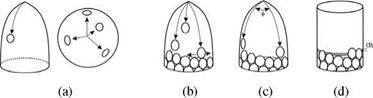
Adler [2] uses a simulation model in which a constant vertical speed of the cells is accepted until these arrive at the border or collide with the other cells. Local repulsion forces between the cells are active, so that these can move now only horizontal, i. e., by modification of the divergence angle (see Fig. 4.17b). Ridley [177, 178] examines the packing procedures with the Golden Section and obtains a good packing, as long as a divergence angle of ф is kept and the vertical offset (misalignment) of the objects is computed from their surface A. The surface is transformed into a ring around the branch with radius R, and so determines the modification of the height for the next object, while ring after ring is placed around the branch for each new object
A
A = 2nRds ^ ds =——. (4.1)
2nR
Although this also does not represent an explanatory model, it is, however, a simple and effective method for computer-assisted modeling of the phyllotaxis along cylinders.
Fowler et al. [67] describe a similar method that, however, is collision-based. In this process cells are produced with a divergence angle of ф and are only vertically mobile. They move so to the border, until they collide with other cells (see Fig. 4.17c). Due to the given divergence angle we are actually dealing here with a mixture consisting of an explanatory and a description model. Unfortunately the authors do not specify whether a variation of the angle, in combination with a horizontal shifting, allows for similar models to be generated.
Meinhardt [137] explains a number of biological patterns with the help of locally distributed promoting and restraining substances (reaction-diffusion model). For the production of an array according to the Golden Section, he designed a system with two spatial antagonists and one inhibitor. The system
produces the desired array pattern along cylindrical geometries; however, it is susceptible to disturbances. Bernasconi [15] obtains sturdier examples with an inhibitor in the space domain and an additional one in the time domain.
