Phyllotaxis is the term for the regular arrangement of outer plant organs such as leaves, blossoms or seeds along branches or in a bud. In Sect. 2.1 the distribution of leaves along the shoot axis was already discussed, and in the preceding section similar distributions of compound leaves were found.
The arrangement of the leaves is here often subject to a law, that was probably among the earliest found correspondences between the botanical processes, Golden Ratio ^ their mathematical description, and the resulting aesthetics: the Golden Ratio.
A classical example of an emerging pattern is the distribution of the seeds in a sunflower.
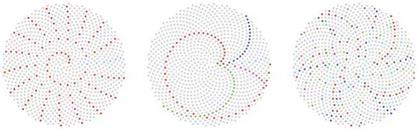
The arrangement of the seeds is the result of an optimization process, that arranges the seeds as closely as possible on a circular disk. The sample computer image of Fig. 3.5 is computed from the application of a simple rule that was proposed by Vogel [226]. The ith position of the grain is described in polar coordinates by the angle a* and the radius r*. It results from the following rules:
r* = c ■ лД a = i ■ ф. (3.8)
Here c is a positive constant and ф must have the following value:
ф = = 137.5077…° with т = ^+1. (3.9)
t 2 2
The value for т is here the relationship of the Golden Section, which since antiquity has been especially known to be a convenient proportion ratio for partitioning. The radial shift over the square root in Eqn. (3.8) is geometrically motivated, since with more dense packing the number of placeable objects on a circular disk is proportional to their surface and thus to r2. Hence, inevitably, with progressive placement, growth according to the square root of the radius must take place, in order to ensure an even positioning.
In Fig. 3.5 the developing arrangement sequence is represented as well as three examples, which show the behavior of divergence angles in the proximity of ф. If the angle is minimally changed, a distinct striping results, and in the case of expanded objects, such as, for example, the sunflower seed, a worse packing density will occur.
Less understandable than the choice of the radius is, at a first look, the choice of ф = 360/т2. Here the division ratio corresponds to the Golden Angle substantially more clearly if one utilizes an additional characteristic of т: [2]
|
ч- ф = 137.20 (b) If, instead of ф, a divergence angle of 222.4922…° is chosen, an inverse arrangement of the elements according to the Golden Angle is obtained. The spiral now “turns” counterclockwise. Although the developing distributions are very balanced, a set of spirals (paras – tichies) can be identified, which run either in or against the clockwise direction (see Fig. 3.5). Despite the symmetrical appearance of the image, 21 paras – tichies run in the clockwise direction, but 34 run inversely. The differences between neighboring elements on the spirals behave accordingly, at least on the outer part of the pattern. On the spirals running in the clockwise direction, two neighboring dots have a difference of 21, on the ones moving in the opposite directions, the difference is 34. Out of a larger number of dots new parastichies with other neighboring conditions are formed. The reader should not, however, be fooled. Alan Turing (1912-1954), one of the fathers of computer science, attributed this strange phenomenon to the characteristics of the human eye by postulating, that all possible parastichies are contained in the pattern of the Golden Angle; in some areas they only appear visually more strongly than in others. Astonishingly, the differences among the parastichies form the sequence of Fibonacci numbers (named after Leonardo Pisani (1160-1250), called Fibonacci), wherein each number is produced by the sum of the two previous numbers: f = 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Still another connection between the Fibonacci numbers and the golden section: Johannes Kepler (1571-1630) noticed that the ratio of consecutive Fibonacci numbers approaches the Golden Ratio. Therefore the angle of the Golden Section also often is called the Fibonacci Angle.
|
|
|
it should at this point be noted that the phyllotactic patterns presented here are purely descriptive models. A plant does not compute itself according to a fractal model and a flower is never able to keep the required high accuracy of the divergence angle in the arrangement of its seeds, which would be necessary for the positioning of the Golden Ratio. These are mathematical models that describe the appearance amazingly well, but state little about the actual synthesis.
Here functional models must be found. An example is a model that produces the appropriate pattern formation in the flower by local optimization of the packing density (see Sect. 4.13). Other functional models are illustrated in the next chapters where we discuss the synthetic production of plants. In some cases, the physiological simulation of plants leads to interesting results. Often descriptive models are also used because with their help real-looking geometries can be produced, without taking into consideration the underlying biological model.
We now turn to plant populations and their description. The elements that have to be described here are no longer branching structures, but dots or small areas on the plane, which mutually affect each other.
