![]() The general mechanism of a rewriting system can best be illustrated with the so-called snowflake curve or von Koch curve. This curve is actually the classic example of a rewriting system, and, therefore, it is found in many places in the computer science literature. Rewriting takes place graphically: each edge of a given geometry is replaced by a sequence of edges. The rewriting method is implemented using a so-called generator (see Fig. 5.1a). The successive application of generators on the edges of the initial object, the initiator, results in a complex figure, which resembles here the outline of a snowflake.
The general mechanism of a rewriting system can best be illustrated with the so-called snowflake curve or von Koch curve. This curve is actually the classic example of a rewriting system, and, therefore, it is found in many places in the computer science literature. Rewriting takes place graphically: each edge of a given geometry is replaced by a sequence of edges. The rewriting method is implemented using a so-called generator (see Fig. 5.1a). The successive application of generators on the edges of the initial object, the initiator, results in a complex figure, which resembles here the outline of a snowflake.
|
|
|
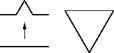
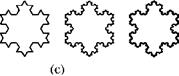
As already mentioned, graphical rewriting is just one option for the definition of a rewriting system. There are a number of different methods used for various purposes:
■ Graphs
Here edges and nodes of a graph are replaced by subgraphs (see [27]). The original graph is in this way enlarged step by step. The underlying mechanism uses grammars that specify the rewriting rules. In Sect. 5.13 a similar method is outlined that works, however, with textual rules.
■ Cell Grids
Values or value combinations in a cell are replaced with other values. An example is “The Game of Life” (see [70, 71]), which produces complex spatial patterns using simple rules (see also Sect. 4.1). Similar mechanisms are used for the modeling of plant populations and other processes [116].
■ Text
In the already mentioned L-systems, characters in a text are replaced. The mechanism was introduced by Thue (see [185]). Chomsky [26], a linguist, compiled a concept for the description of languages using so-called formal grammars with alphabets, axioms and productions, which incidentally is also the basis for the Lindenmayer systems.



