Static LOD Methods for Trees

The appearance of trees is mostly determined by the foliage, so that methods have to achieve an optimal approximation for the many isolated surfaces of the leaves. The problem here is the special characteristic of the foliage, since, in contrast to smooth surfaces, the approximation should not reveal a smoothness but rather the fringed outline of the crown.

In an earlier study, Gardner [69] approximated trees and terrains with a few ge­ometric primitives. He used quadrics, i. e., surfaces that can be described with square functions such as paraboloidal or hyperboloidal functions. Here proce­dural textures control the color and the transparency of the surfaces. Similar methods are used in a number of computer games in order to illustrate foliage. However, this modeling method often causes an unrealistic appearance, since it is noticeable that the trees were modeled using a set of closed surfaces. Marshall et al. [129] try to avoid these shortcomings by combining a polygo­nal representation of larger objects with tetrahedral approximations of smaller objects. Here the important large objects are represented detailed, while the smaller ones are being approximated. However, the problem of the unrealistic appearance is also here still present.

Max and Ohsaki [134] blend the polygonal model description with images of trees or parts of trees that were computed beforehand. Since these images are again generated from already-produced models, the authors are able to receive important additional information: the depth value of each pixel from the di­rection of the virtual camera position. If the model should be shown from a slightly modified camera position, this can be done through the reprojection of these pixels with depth. The method is one of the earlier studies of the already – mentioned image-based rendering, in which a computer image is not generated through the projection and rendering of a polygonal geometric description, but rather directly from existing image information.

The function, mathematically seen, determines the transformation between the pixel coordinates of the already rendered image (x, y,z) where the x, y are coordinates describing the pixel positions in the image and z is the respective depth value, and the pixel coordinates (x’, y’, z’) of the desired new viewing position; this is an affine mapping. It can be executed through the multiplication of the pixel position in the form of homogeneous coordinates with a 4×4 matrix M (see [230]).

The computation of the image values for a virtual camera takes place through a perspective projection of the world coordinates into the camera coordinate sys­tem. This is also accomplished with an affine transformation that is described by a matrix C. The matrix M for the calculation of the desired camera position C2 is now obtained by

M = C2 C-1. (10.1)

A problem in combination with the reprojection is the occlusion of pixels. Since in the initial image always only one value can be stored for a pixel, in the reprojection we find spots for which there is no image information (see Fig. 10.2). A procedure that lessens these problems is rendering of the initial object from many different directions, and then combining several of these original images for the production of a new image. In [134], for example, 23 original images are used in order to obtain satisfactory results.

Figure 10.2 Reprojection: the image data from one viewing angle is transferred to another viewing angle

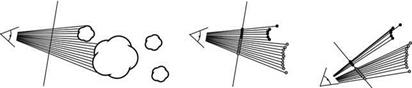
The problem of lacking image information as well as the need for a high mem­ory capacity can be decreased through a hierarchical approximation [131,132]. Here the tree is not approximated through image information as a whole, but rather by approximating the single primary and secondary branches. Results of this method are shown in Fig. 10.3.

For a strict hierarchically constructed tree with only one branch geometry in each level that is arranged along the trunk and produces branch geometries via recursive replication, the method can be written as follows:

■ Generate a leaf through a textured polygon with the image of the real leaf.

■ Generate a twig through combinations of leaves. Generate an image-based description of the branch geometry from several images with depth values.

■ Produce branch through combinations of the descriptions of the twigs as images. Produce an image-based description of the whole branch.

■ Generate a tree description through the combinations of the branches. Gen­erate an image-based description of the whole tree.

For rendering of a camera path in the direction of the tree, a hierarchical de­scription with details relative to the projected size must be generated. In [131] this is realized in software, while a hardware-oriented extension for recursive trees with several branch and twig types is presented in [132]. The rendering takes place in the following way:

■ For the distant viewing positions render the tree from the combination of the images of the total object.

■ Starting at a distance threshold, replace the representation through the com­bination of the reprojected images of the single branches together with the (polygonal) trunk.

■

For the detailed images, replace each of the visible branches through a combination of the reprojected images of the smaller branches, and so on.

Similar methods of approximations with images originate from Schaufler and StUrzlinger [190]. So-called impostors – representations of complex geometry in the form of successively positioned images with depth information – are here reprojected. A similar technique is used by Perbert and Cani for the interactive rendering of meadows [156].

Instead of storing the depth information of the pixels explicitly using volume textures this can also be handled implicitly. Just like a single image that is the discretized representation of a surface, a voxel description is the discretized representation of a volume. If a pixel equals a square base element of an image, then a voxel equals a cubic base element of a volume. In computer graphics, volume data can be stored using volume textures [104] that represent a set of parallel arranged textures in a space. Each texture is allocated a uniform depth, and the image information of the texture describes the corresponding voxel values of the respective plane in the volume.

In contrast to classic volume rendering, a volume texture, however, only exists close to the surface of the given model, and thus permits in this way an essential reduction of the data. If model parts are instanced and deformed, then this takes place also via the volume texture. In addition to common voxel data, here further parameters such as reflection attributes in the form of the BRDF are stored.

Neyret worked extensively with volume textures for the rendering of plants [148,147,149]. Through the application of hierarchical texture representations and the respective rendering methods, he was not only able to produce faithful­looking landscapes relatively quickly, but also to represent complex light and shadow interactions realistically.

Chapter 10 Figure 10.4 shows two landscapes that were produced through hierarchical ren – Level-of-Detail dering. The rendering in video resolutions takes about 20 minutes with a R4400

processor at 200 MHz. An acceleration of the method is proposed in [140], and a similar approach for volume rendering of forests was introduced by Chiba et al. [25].

Shade et al. [195, 196] introduce a cascaded representation method for plants in complex outdoor scenes. The goal here is to also render large landscapes in real time through carefully coordinated static level-of-detail descriptions. In their system distant plants are represented using billboards. Closer objects are approximated using images with depth that are obtained through reprojec­tion. The next detailed model description that is used is a dynamic point-based method that represents an extension of the images with depth. These methods will be introduced in the next section.