Tree Modeling Using Strands

Leonardo da Vinci assumed that for trees in a branch bifurcation, the cross­section of the father branch equals the sum of the cross-sections of his children. This was already discussed in Sect. 3.3. Likewise we already mentioned that this estimated value was proven to be amazingly precise.

Figure 4.13 Tree model using strands: a) combination of strands in a tree; b) branching parameters

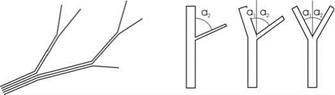
This realization, combined with the knowledge about the vascular internal structure of trees, prompts to define the whole tree structure using small strands, which would reach from the root of the tree up to the leaves. In a forking, the strands are divided and continue to run further along in the children. If a close packing is present, then the above cross-section ratio is obtained.

Matthew Holton [89] modeled trees according to the above procedure (see Fig. 4.13a). The number of strands here not only determines the thickness of the branches, but also their length and the number of leaves as well as the branching angle.

Should a branch bifurcate with S0 strands, where the ratio of the strand num­bers of the branches is given by Pg, w, in reference to the botanical order num-

bers from Sect. 2.3, then for the numbers of strands Si, S2 in the children we apply

51 = 1 + Pg, w(So – 2),

52 = 1 + (1 – Pg, w)(So – 2).

The diameters of the branches are computed using di = Ty/Sl, where T is a constant. The result is the required relation between the cross-sections:

d2 = d2 + d2.

The branching angles a1 and a2 (see Fig. 4.13b) are calculated considering the entire branching angle AG, W using

S2 A ai = Ag, w S0	a2 = Ag, w — ai
The lengths of the branches are also computed from the strands, whereby the ratio of the root functions of the strand numbers is used:
Ri = ^sI/^So,	Li = Ri Lo,
R2 = VS2/VS0,	L2 = R2 L0.

At this point, the parameters provided by the user are added. Holten differenti­ates between the characteristic length Li and the active length li appearing in the model.

Figure 4.14 Examples of tree models generated using strands (Courtesy of M. Holton)

While the characteristic lengths of the children are computed from the lengths of the parents – thus representing here a hierarchically defined characteristic of the model – the active lengths are independent of the other active lengths. However, the characteristic lengths of the respective fathers do apply. For both lengths, maximum values and minimal values have to be entered by the user. The results are shown in Fig. 4.14. The pine trees were generated each with 2500 strands. Here for the branching ratio and angles the following values are assigned:

All other parameters can be found in [89]. Holten also states that for the model­ing of the pine tree shape seen in Fig. 4.14b, further boundary conditions were used, although he did not define those.