The theory of fractals allows for new mathematical ways to describe a number of natural objects. At this point, however, we cannot discuss the formalism or the consequences of the fractal theory in general, we are merely sketching the description of botanical branching structures as fractal objects. For a more in-depth review see Mandelbrot’s well-known book “The Fractal Geometry of Nature” [127].
After we have reviewed and analyzed the topology of branching structures in the last two chapters, geometry comes now into play again. A small part of a tree (a branch or a twig) looks similar to the entire tree. This also applies to many mountain formations, coastlines and crystals. Mandelbrot calls such objects fractals. An essential term in this connection is therefore the selfsimilarity of an object.
While the topological dimension DT of all curves has the value one, their Euclidean dimension E can also take the value two, whereby the curve is no longer differentiable at any place. Such non-differentiable curves led, after a work by Du Bois Reymond in 1875 [50], to completely new aspects in classical mathematics, whose research opened the way to a set of new formalisms and applications.
Hence, aside from the Euclidean dimension, still further dimension definitions can be found, with which such “monster objects” can be described. This allows us to quantify their characteristics. In this process, the self-similarity of objects can be used as well.
|
|||
|
|||
|
|
||
|
|||
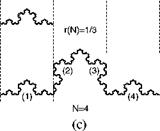
A distance of length L, thus an object of Euclidean dimension one, can be divided into N parts, whereby one can obtain each part from the whole using the scaling S = r(N) = 1/N (see Fig. 3.3a). For a square one needs a scaling r(N) = 1/N1/2 and for a cube r(N) = 1/N1/3. For higher-dimensional cubes we find
|
|
|
|
|
|
|
|
D =_____ ^°g N. (3.3) Section 3.3
log r(N) Trees as Fractal Objects
It is also possible to understand D as the dimension of the self-similarity of an object. The self-similarity of a square or a cube is not particularly exciting.
More interesting is, for example, the von Koch curve (snowflake curve) from ^ similarity dimension Fig. 3.3c, because here we obtain a value D = log4/log3 « 1.2618. Each quarter of the object must be scaled by a factor of three, in order to become similar in its form to the whole.
In contrast to cubes, the similarity dimension exceeds here the topological dimension of the object, in this case the object is termed a fractal. Besides fractal curves such as the von Koch curve there are also fractal point sets (DT = 0) and various higher-dimensional fractals.
The fractal analysis of a tree can be carried out in two different abstraction levels. First we only look at the tree skeleton, whereby the thickness of the branches and the trunk are neglected. In the second step, we also incorporate the diameter of the trunk and branches.
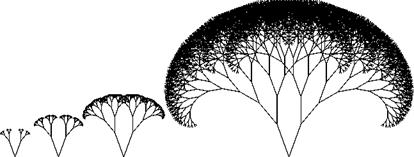
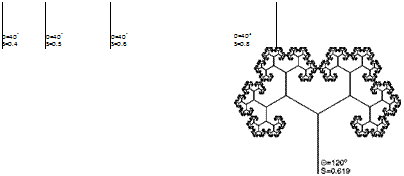
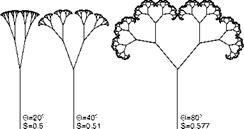
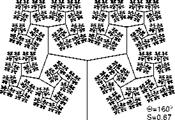
As an example, in the top line of Fig. 3.4 some fractal tree structures are illustrated that have the same branching angle 0 but different scaling factors S of branching lengths relative to the father branch. Thus, the necessary scaling r(N) varies as well as the similarity dimension of the tree skeleton. The angle 0 is constant for all branching levels, which represents a rather rough approximation of the botanical law. In the lower lines of Fig. 3.4, 0 was varied and selected in such a way that in each case the branches do not overlap.
For the mathematical analysis, the tree is divided into two different parts, into the quantity of the branch tips and those of the branches itself. The first part is an isolated point set (a dust) and has the dimension DT = 0. The branches, with or without branch tips, form topologically a curve with DT = 1.
With regard to the fractal dimension the point set of the branch tips needs N =
2 for r(N) є ]0…yi/2], thus it has a similarity dimension D є ]0… 2]. Thereby the angle of the branching can vary within a large range, without changing the dimension. The same D allows thus for a multiplicity of tree shapes (see [127]).
However, Mandelbrot used in his analysis of the fractal dimensions the so – called Hausdorff-Besicovitsch dimension, for self-similar objects that equals the similarity dimension, but yields meaningful results for a larger quantity of objects. The Hausdorff-Besicovitsch dimension is considerably more difficult to define and to compute than the similarity dimension. Mandelbrot uses the terms “fractal dimension” and “Hausdorff-Besicovitsch dimension” as synonyms; this may be permitted here also for the similarity dimension, although mathematically it is perhaps precarious.
Let us return to the tree examples: The scaling factor S of the branches with regards to the sizes of the respective father branches plays an important role.
It determines directly the fractal dimension of the branches, but also those of the branch tips. For S > 1 the tree is unrestricted and the fractal dimension of
the branching sinks below one. For smaller values of S the branching angle 0 “
 |
|
|
|
|
|
must always be selected to be larger in order to avoid self-overlapping (see Fig. 3.4); the fractal dimension in this case exceeds one. The values S = yJl/2 and 0 = 180° yield a plane-filling tree with D = 2.
If one examines real branching structures somewhat more closely, then interesting differences regarding the thicknesses of the branches are found. Leonardo da Vinci (1452-1519) assumed a connection between the thickness of a branch d and the thickness of its children dl, d2. He postulated that the sum of the cross-section areas of the children in a branch equals the cross-section area of the father branch [33]. Thus
d2 = d^ + d2, (3.4)
which later was proved to be an excellent estimated value for botanical trees. Unfortunately, the result is that botanical tree skeletons are not self-similar, at
|
tree height3 ————- Tf = const. trunc area2 |
least not if the thickness of the branches is considered. If Eqn. (3.4) is generalized to
dA = dA + dA,
for self-similarity Д = D must be selected. This relationship holds, for example, for the bronchial tree of the lungs, where Д = D = 3 applies. Arteries have Д « 2.7 and river systems Д = 2.
For the most botanical trees Eqn. (3.4) with Д « 2 applies, which has been confirmed by many empirical investigations. Since they are almost space filling, D « E = 3 (see also [127]) can be assumed. Thus, in contrast to the bronchial tree they are not self-similar. And indeed a small branch is similar to a large tree; it possesses, however, a trunk that is too thin. Another result of Д = 2 is that a botanical tree, in contrast to a bronchial tree, is rather translucent. It is possible to look through a botanical tree, but not through a bronchial tree, as stated by Mandelbrot.
A beautiful illustration of the geometrical coherencies is given if one imagines each leaf to be connected with a root through a strand. The sum of the strands in a branch determines its volume and diameter, the relationships between the branch diameters and the diameters of their father branches in this case yield the values given by Da Vinci. This idea is implemented later in Sect. 4.10 in an algorithmic approach to the production of tree geometries.
The specific values of Д and D for botanical trees can be reduced, according to Halle, Oldeman and Tomlinson [81], to the problem of the energy exchange: the problem of the energy exchange in trees can be simplified by considering the tree as a system in which with a minimal production of volume as much as possible surface must be provided with water, and which at the same time guarantees the transport of the absorbed energy. To obtain a maximum of surface with a minimum of volume leads almost inevitably to fractal structures.
In contrast to a bronchial tree or to arteries, a tree is not supported from the outside, but must carry itself and also must resist the influence of wind. Therefore the structure must be lighter than that of the bronchial tree and we assume Д C 3. The integral values for D and Д result here in a coherence, that can again be empirically proven.
As an example, the total surface of the leaves of a branch proportionally relates to both the volume within the outlines of the branch and the diameter of the branch, this (according to [127]) was empirically affirmed by Huber in 1928. Further results are
(3.6)
|
diameter of space occupied by a branch3 |
 |
 |
For each branch it follows:
since the wind resistance of a tree is approximately proportional to the branch and leaf surface and thus to the third power of the height, while the resistance
Chapter 3 of a branch is proportional to the square of its diameter, the need automatically Some Mathematics arises for a connection such as that in Eqn. (3.6).
