A modern industrialized state is extremely complex, heavily dependent on a steady supply of raw materials. Most materials are being produced at a
|
Table 2.2 The water demands of energy |
|
|
Energy source |
Liters of water per MJ |
|
Grid electricity |
24 |
|
Industrial electricity |
11 |
|
Energy direct from coal |
0.35 |
|
Energy direct from oil |
0.3 |
rate that is growing exponentially with time, at least approximately, driven by increasing global population and standards of living. So we should look first at exponential growth and its consequences.
If the current rate of production of a material is P tonnes per year and this increases by a fixed fraction r % every year, then
Integrating over time t gives
where P0 is the production rate at time t = t0. Figure 2.8, left, shows how P grows at an accelerating rate with time. Taking logs of this equation gives
so a plot of log10(P) against time t, as on the right of Figure 2.8, is linear with a slope of r/230.
Figure 2.9 shows the production of three metals over the past 100 years, plotted, at top, on linear scales and, at bottom, on semilog scales, exactly as in the previous figure. The broken lines show the slopes corresponding to growth at r = 2%, 5%, and 10% per year. Copper and zinc production has grown at a consistent 3% per year over this period. Aluminum, initially, grew at nearly 7% per year but has now settled back to about 4%.
Exponential growth is characterized by a doubling-time tD over which production doubles in size. Setting P/P0 = 2 in Equation 2.2 gives:
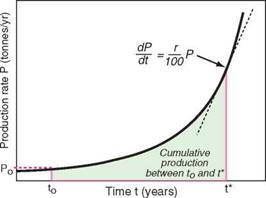 |
FIGURE 2.8
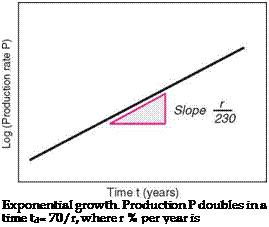 |
the annual growth rate.
The cumulative production Qt between times t0 and t* is found by integrating Equation 2.2 over time, giving:
This result illustrates the most striking feature of exponential growth: at a global growth rate of just 3% per year we will mine, process, and dispose of more "stuff" in the next 25 years than in the entire 300 years since the start of the Industrial Revolution. An alarming thought, pursued further in Exercise E.2.5 at the end of this chapter.



