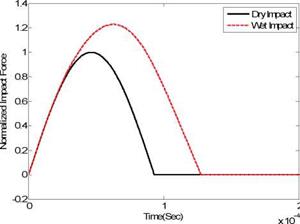
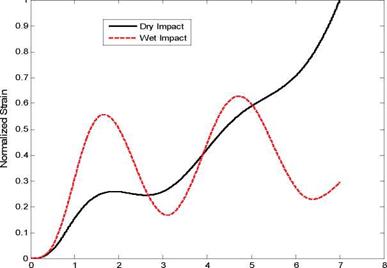
First of all, the impact force is computed from the models described in the previous section and compared between dry and wet impact cases in Fig. 12. The computer modeling and simulation with an impact energy of 0.5J produced a result qualitatively agreeing with the experimental observation as plotted in Fig. 5. Because of FSI, the wet impact results in a
higher impact force than the dry impact. The FSI produces an added mass effect, which makes the structure under water move slower than the same structure in air. Such a slower movement yields a higher contact force between the impactor and the structure.
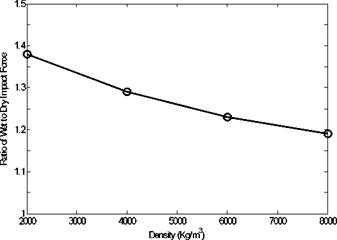
A parametric study is conducted to study the effect of different material properties on the peak impact force ratios between the wet and dry impacts. The first parameter is the structural mass density. As shown in Fig. 13, the structural density significantly affects the wet impact force. As the structural mass density becomes smaller and more comparable to the water density, the added mass effect gets greater. Therefore, the peak of the wet impact
|
Fig. 12. Comparison of normalized impact forces between dry and wet impact modeling of a composite beam |
|
Fig. 13. Plot of effects of beam density on ratios of peak impact forces between wet and dry impact models |
Modulus (GPa)
becomes much greater than that of the dry impact for a lighter structure. This suggests that wet impact is more critical for polymer composite structures than metallic structures because polymer composites have much lower mass densities than conventional metals. On the other hand, a change of elastic modulus of the structure has only a minor effect on the wet impact force as shown in Fig. 15. In other words, the ratio of the wet to dry peak impact forces does not vary much with respect to the change of structural modulus.
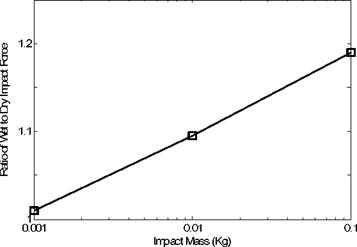
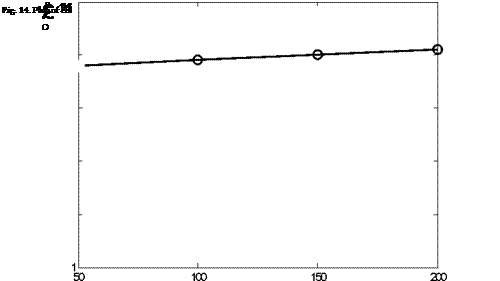
Because the previous experimental study also indicates the ratio of the peak impact force between the wet and dry impacts is affected by the impact energy, as the impact energy becomes smaller, the FSI effect also becomes lower so that the impact force ratio approaches unity. This fact is also supported from the numerical study. In the numerical simulation, the impact mass is varied in the finite element model in order to change the impact energy. The maximum contact force under wet impact loading is computed for different impact energy (i. e. impact mass) and the value is normalized in terms of the maximum contact force under dry impact with the same impact energy. The results are plotted in Fig. 16. As shown in the figure, the impact force ratio approaches to unity as the impact mass becomes 0.001.
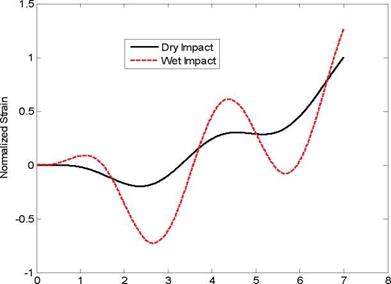
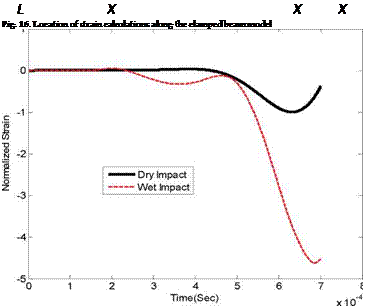
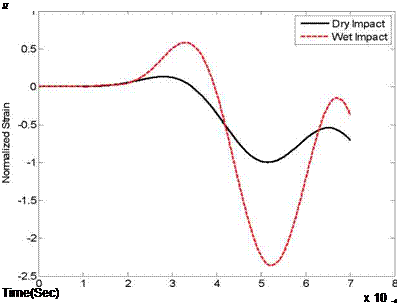
Another application of the computer model is to investigate the effect of FSI under impact loading on the strain histories of the structure. Because the FSI effect is not uniform, the experimental study indicates that the strain near to the boundary is more influenced by the FSI effect. This fact is also investigated using the numerical model. Fig. 16 shows the locations of the beam where the strains are computed. Figures 17 though 20 plot the strain histories of the wet and dry impacts, respectively. The plots are normalized with respect to
![]()
|
1 2 3 4
![]()
 |
|
|
|
the respective dry impact strain. Comparing those strains tells clearly Location 1 has the greatest difference of strain histories between the wet and dry impacts. In other words, the FSI effect with impact loading is greater at the location near to the clamped boundary.
3. Conclusion
Both experimental and numerical studies are conducted to understand the effect of FSI with impact loading on polymer composite structures. For an experimental study, an experimental set-up is designed and fabricated for impact testing on composite plates submerged in water. In order to investigate the transient dynamic response of composite plates with FSI effects under impact loading; three impact conditions, dry, air-backed wet, and water-backed wet impact conditions are considered, respectively. In order to focus on the FSI effects on the transient dynamic responses, impact loading is controlled not to cause any damage to the composite plates. Since the composite material has a very comparable density to water, the FSI effects are very significant on the impact force and transient responses of the plates. Due to the added mass effect of water, the impact force is much greater for the wet impact cases than for the dry impact. Similarly, wet impact produces much greater transient strains on the composite plates. As a result, the wet impact is more detrimental to the structure than the dry impact. However, the increase of magnitude of transient strain responses resulting from the FSI with wet impacts varies significantly. The transient strain responses depend on the location of the composite plate because the added mass effect is not uniform over the plate. The location near to the clamped boundary corner has generally a greater FSI effect on the transient strain response. Comparison of AVMIF
between the composite and steel shows approximately 3 to 5 time greater values for composites than steel, which indicates a much greater effect of FSI on the composite than steel.
The numerical modeling and simulation confirms the experimental observation. Wet Impact loading on a composite structure produces a much greater impact force than dry impact. However, as the impact energy becomes smaller, the peak wet impact force becomes closer to that of the dry impact force. A numerical parametric study also indicates that density of the structure significantly influences the FSI effect of the wet impact. If an impacted structure has a low density like a polymer composite, the FSI effect on impact loading is larger while the effect is less for a structure made of a conventional metal. On the other hand, the elastic modulus of the structure has a negligible change in the FSI effect with impact loading. Furthermore, both experimental and computational studies show that the FSI effect with impact loading is not uniform and greater near to the clamped boundary.