1.2 Analytical procedure
Rose’s analytical model (Rose, 1981 and 1982) is used to compute the SIF for the repaired plates by single patch,
Kr=Y- <r0/Vk (12)
where Y is a geometric factor, which accounts for repairs to center or edge cracks; Y=1 for a repair to a centre crack; oo is the nominal stress that would exist in an uncracked plate after the application of a patch:
![]()
![]() Aa
Aa
°° = 1+5
where S=ETtT / Eptp. k represents a spring constant given by:
k – &
(1+5)(l-vp)
where в is a shear stress transfer length in a representative bonded joint:
In the case of one sided repairs, Ratwani (Ratwani, 1979) provided a bending correction factor:
K*=(1+BC)KR (16)
where K’R is the stress intensity factor for a one sided repair, the correction term BC is given by:
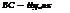
![]() (17)
(17)
|
where ymax is the distance of the extreme fiber ply from the neutral axis of the cracked plate: |
|||
|
Утах |
-tp+Z |
(18) |
|
|
with |
|||
|
z = s(t |
} + tr+2ta) 2(1+5) |
(19) |
|
|
and I is the total moment of inertia of the plate repair: |
|||
|
I — Ip + ulr |
and n = — EP |
(20) |
|
|
where |
|||
|
Ip — wpj |
– + wptpZ2 |
(21) |
|
|
t? lr=wr 12 + wrtr- |
| + ta + (|-Z) |
2 |
(22) |
|
4 |
|||
|
The stress intensity factors, computed with the above mentioned analytical procedure, for the different patch configurations (i. e. fiber lay-up and adhesive type) are shown in the Tables 7. |
|||
|
Specimen Configuration Analytical K*R fMPaVm] |
FEM K*r fMPaVm] |
Difference [%1 |
|
|
Test 1 – repaired plate: |
|||
|
patch type 1 + ad. EA956 |
8.62 |
8.32 |
-3.6 |
|
patch type 1 + ad. FM73 |
8.97 |
9.22 |
2.6 |
|
patch type 1 + ad. AF163-2K |
9.12 |
9.54 |
4.4 |
|
patch type 2 + ad. EA956 |
10.15 |
9.95 |
-2.0 |
|
patch type 2 + ad. FM73 |
10.4 |
10.91 |
4.7 |
|
patch type 2 + ad. AF163-2K |
10.5 |
11.24 |
6.6 |
|
Table 7.1. Analytical and numerical SIF for the repaired plate in Test 1 |
|||
|
Test 2 – repaired plate: |
|||
|
patch type 1 + ad. EA956 |
12.92 |
12.51 |
-3.3 |
|
patch type 1 + ad. FM73 |
13.46 |
13.87 |
2.9 |
|
patch type 1 + ad. AF163-2K |
13.67 |
14.35 |
4.7 |
|
patch type 2 + ad. EA956 |
15.23 |
14.98 |
-1.7 |
|
patch type 2 + ad. FM73 |
15.59 |
16.43 |
5.1 |
|
patch type 2 + ad. AF163-2K |
15.75 |
16.94 |
7.0 |
|
Table 7.2. Analytical and numerical SIF for the repaired plate in Test 2 |
|
Test 3 – repaired plate:
Table 7.3. Analytical and numerical SIF for the repaired plate in Test 3 4.2 Numerical procedure A finite element analysis of the configurations of Fig. 4 is carried out using the finite element code Franc2D/L for the total structure (plate and patch). The patched plate is meshed using standard two-dimensional six node isoparametric elements with triangular shape. The repaired structure is modeled as three layer structure (plate, patch and adhesive). Due to the symmetry of the problem, only half plate is modeled using 29373 nodes and 14578 elements. Tables from 7.1 to 7.3 report the SIF obtained with the finite element models and the comparison with the previous analytical results. The configuration with the adhesive AF163-2K usually demonstrates the highest difference between numerical and analytical values. This performance is due to improved atomic bond of the glue. The adhesive AF163-2K has the lowest elastic and shear moduli. The patch type 2 always provides a higher SIF and among these configurations those using the adhesive AF163- 2K are the highest. |


