The proposed method

Concurrent Engineering imposes that the design of the manufacturing and the assembly jigs, of the manufacturing and assembly cycles, be in the same time of the product design. In fact, only the concurrent design of the final product, of the single components, of the manufacturing processes and jigs, of the assembly cycle and jigs and of the inspection procedures assures to achieve a high quality with the smallest costs.

The proposed method adapts the steps of the tolerance analysis process suggested by the

eM-TolMate® package and described in the previous paragraph to the case of an assembly

involving non-rigid freeform surfaces in composite material. It is constituted by the

following 7 steps:

a. Verify the stiffness of the assembly components. Non-rigid parts may be subjected to significant distortion after the removal of manufacturing forces. This condition, known as free state variation, is principally due to weight and flexibility of the parts and the release of internal stresses resulting from fabrication. This distortion is acceptable if the part surfaces remain within the indicated tolerances, once the part is coupled to another part of the final product by applying reasonable forces. Therefore, the first step of the proposed method is to analyse the internal stress and the relative strain of each assembly components due to the assembly sequence, since those components have freeform surfaces of a small thickness in composite material. This means to simulate the assembly configuration of each assembly components through a fixturing equipment on a coordinate measuring machine and, then to measure the displacements from the nominal configuration represented by the CAD model through an inspection process. This is true if the effect of the inspection process on the measured deviation is indeed non significant and this hypothesis needs to be verified. The displacements between the real part and the nominal one, obtained in the inspection process, may be used as input values for a structural numerical analysis with the objective to obtain the stress and strain fields induced in the material when the part is assembled in the final product. The numerical analysis may be carried out with a Finite Element Method®, but before implementing the real case simulation, an assessment of the software capability on composite material is required through a simple 2D case study. If the results of the numerical analysis demonstrate that the deformations induced by the assembly sequence are at least of an order of magnitude smaller than the applied tolerances, the part may be considered rigid and the models or software of the traditional tolerance analysis literature may be applied. In this way the complexity to consider the compliant of the assembly components may be avoided.

b. Design the measurements of the assembly. A first analysis of the assembly working allows to identify all the functional requirements that the product should perform. This means translating the functionality of the design assembly in all the couplings or kinematic constraints among assembly components that are needed for the assembly to work correctly. Then, the pairs of assembly components involved in each functional requirements are defined. The features of each pair of components, that are involved in each functional requirement, are identified and are generally assigned to them a set of tolerances. Therefore, the functional requirements and the assembly constraints are translated into measurement of the assembly, while the coupling parts and their feature are passed to the following step of the method. A widespread measurement in aeronautic field is the distribution of the minimum distances along two faced freeform surfaces, e. g. when the adhesive thickness between the faced parts to connect should be as constant as possible in order to obtain an efficient structural connection and to avoid local compressions at the interface of faced parts due to strong reduction of thickness. In this case it has been demonstrated that the minimum distance among the two patterns of points, belonging to the two faced surfaces, calculated by projecting the point to point distance along the direction perpendicular to the nominal surfaces is very near to the minimum distance and it is easy to calculate by eM-TolMate® (Polini et al., 2007).

c. Define the features of the assembly components, specify the tolerances and the related statistical distribution. The features of the coupling parts of the assembly may be free-form surfaces or basic surfaces. The free-form surfaces of each assembly components have to be schematically represented by a set of control points. The number and distribution of the control points depends by the slope of the free form surface. If two freeform surfaces are faced, the pattern of control points of the second surface may be obtained by intersecting the second surface with the pattern of vectors, that are normal to the first surface in each control point. The tolerances applied to the freeform surface should be applied to each control point defined on the surface. The basic surfaces are plane, pin, hole, point, tab, slot, constant profile surface, constant cross section, sphere, surface of revolution, general 3D surface, edge features and derived features. Dimensional tolerancing is supported as +/- tolerances (symmetric or not, sizes or distance from an origin feature) and for size tolerances of pins, holes, slots and tabs. Tolerance attributes can be freely modified to reflect effectively the parameters of actual features. The most common attribute is the tolerance probability density function for each tolerance applied to each feature of the assembly component. The probability density function depends by the manufacturing process of the feature and it is generally hardly to estimate. Therefore, the default distribution is assumed to be the Gaussian, since it is symmetric, it is simply to use and it is well known by the literature. However, it is always to change it. Finally, it is needed to verify the datum reference frames (DRFs), the assembly should have its DRF, that is generally considered "global"; while each component should have its DRF, that is considered "local". Moreover, the elements (planes, axes and so on) that constitute a local DRF should be easily identified, manufactured with the design specifications and accessible for verification. The elements of the local DRFs should be qualified by tolerances. The elements of the local DRFs should be used to manufacture, to assembly and to control the assembly components. These simple rules on the definition of the DRFs allow to obtain whose components may be manufactured, assembled and controlled. Obviously, they have to be applied by means of a concurrent approach that is implemented by a designer of product, by a planner of manufacturing processes, by a designer of assembly cycles and by a designer of inspection processes.

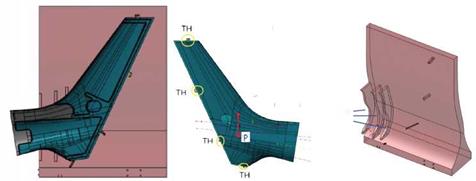
d. Design the assembly cycle and jigs. If required, the assembly jigs should be designed at first. The assembly jigs should have a plane and two pins in order to locate and fix the coupling component. The tooling hole (TH) system is the assembly system that is widespread in aeronautic field and consists in jigs mated with the assembly components by means of pins that are inserted into tooling holes (TH) located on the assembly components. The tolerances of the TH are very critical, since they influence the location and orientation among the different components of the assembly and, therefore, the functional requirements of the assembly. Some suggestions to choice the tolerances of a TH may be found in (Marziale & Polini, 2007).The positioning of a component on its jig is made by the contact of two planar surfaces (one on the part and one on the assembly jig) and the clearance fit between two Tooling Holes (positioned on the part) with the corresponding pins (positioned on the assembly jig), as shown in Fig.

1. The position of the THs has an important role in order to limit the flag waving effect
of the component as regards its assembly jig, since a small change in THs position cause a great variation in the location and the orientation of the part on the corresponding jig due to the large dimensions of the parts. Therefore, the distance among the tooling holes must be as larger as the dimensions of the part increases, but this condition is difficult to achieve in some practical cases. Another important consideration is that it is preferred to position the THs out of the part shape, on appendixes that will be trimmed once the part is assembled, in order to have lower production costs. Through these considerations an assembly jig has to be designed for each part. Each assembly jig has a set of tolerances, since it is realised by manufacturing processes.

supporting

saddles

Fig. 1. Aircraft skin’s jig with tooling hole system

The design of the assembly cycle foresees as first step the location of each component on its designed jig. Each component has micro-movements respect to its jig due to the tolerances of the jig and of the component applied to the coupling system, i. e. to the TH system. These micro-movements influence the positioning of the part and, therefore, they have to be characterized by means of probability density function, such as done for tolerances of the parts. The probability density function depends by the manufacturing process of the jig and the component and by the assembly constraints. It is generally hardly to estimate, since it should involve many experimental tests. The default probability density function is the Gaussian. Therefore, each couple of components is assembled by moving near the related jigs and, then, by putting the constrain elements, such as adhesive, bolts or screws. In this way a sub-assembly more and more complex is generated up to obtain the final product. The positioning of the components and, therefore, the accuracy of the final product, depends by the stack-up function of dimensions and tolerances belonging to the components and to the jigs. e. Choose the simulation runs and carry out simulations. Monte Carlo simulation has been used to reproduce the combined effect of all the assigned tolerances and the component degrees of freedom respect the assembly jigs on the assembly functional requirements. The assigned tolerances and the component degrees of freedom have been simulated by means of the probability density functions assigned in the previous steps. The number of runs of simulation has been fixed at the value for which the estimated mean and standard deviation of the obtained probability density function of each functional requirement achieve an asymptotic trend. A step by step procedure has been adopted to evaluate the simulation runs, the starting value has been 10000 runs.

f. Analyse the results. During the assembly simulation, the results of the measurement calculations are stored in memory. When the assembly simulation is finished, a table containing all the measurement results remains in memory. These results may be exported to make statistical analysis. It is possible to evaluate the distribution of the results of each measurement and, therefore, to calculate the percentage of parts outside the tolerance ranges. Another possibility is to evaluate the reasonable tolerance range to assign to each measuring by starting from its estimated distribution in order to satisfy the tolerance analysis. Finally, a sensitivity analysis may be carried out in order to identify the tolerances mainly affecting each gap trend. The percentage weight of each tolerance has been calculated by evaluating the variance of a measurement aTOT, when all the tolerances are applied to assembly’s components, and the variance of the same measurement aTOT-Ti, once i-th tolerance is not applied to the assembly’s components:

TOT