The buckling of composite plates is treated with specific methods applied to each particular case. This part deals with classical bifurcation and FEM buckling analysis, discusses the relevant plate equations and their solutions and edge conditions for perfect plates. The buckling phenomena mean collapse of the structure at the maximum point in a load versus deflection curve and bifurcation buckling. The way in which buckling occurs depends on how the structure is loaded and on its geometrical and material properties. The prebuckling process is often nonlinear if there is a large bending energy being stored in the structure throughout the loading history. According to the level of bending energy, the buckling of plates can occur in two ways: the first is bifurcation buckling and the second is limit point buckling. Bifurcation buckling is an instability in which there is a sudden change of shape of the structure. A bifurcation point is a point in a load-deflection space where two equilibrium paths intersect. On a load-frequency curve, a bifurcation point can be characterized by the load-frequency curve passing through a frequency of zero with a non-zero slope.
Limit point buckling is an instability in which the load-displacement curve reaches a maximum and then exhibits negative stiffness and releases strain energy. During limit point buckling there are no sudden changes in the equilibrium path; however, if load is continuously increased then the structure may jump or "snap" to another point on the load- deflection curve. For this reason, this type of instability is often called "snap-through" buckling, because the structure snaps to a new equilibrium position. A limit point is characterized by the load-frequency curve passing through a frequency of zero with a zero slope. The load-deflection curve also has a zero slope at the point of maximum load (limit point).
Buckling analysis of a plate may be divided into three parts:
– Classical buckling analysis;
– Difficult classical effects;
– Non classical phenomena.
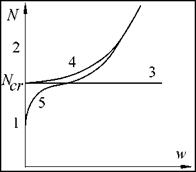
The classical buckling theory may be described by the curve 1-3, from the Fig. AA1 where is plotted the in-plane loading force (N) versus the transversal displacement (w) of a representative point of the plate. By supposing that the loading is applied in the median plane of the plate, no transversal displacement will occur, and in the conditions of perfect symmetry the loading may increase up to the yield point, according to the curve 1-2. At a value over the Ncr, the instability may occur. At N=Ncr one bifurcation point does exist. This means that on the curve loading-displacement, on the path 4, other way, much stable for buckling occurring does exist. At the value Ncr a little perturbation will generate a transversal displacement.
|
Fig. 17.1. Variation of transversal displacement, w, of a plate’s point versus in-plane load N |
The classical linear analysis, which is a generalization of the Euler buckling for beams, should indicate the fact that w increases to infinite at N=Ncr (curve 3). Really, the nonlinear effects started to act and after an initial finite displacement, the in-plane loading N is increasing since the displacement is increasing. In this case the plate is able to carry loads far in excess of Ncr before it collapse. The latest curve (4) is so called a "postbuckling curve" because it depicts the behaviour of the plate after the buckling load Ncr is reached.
The difficult effects in classical buckling analysis are in connection with vibrations, shear deformations, springs, non homogeneities and variable thicknesses, nonlinear relations between stresses and strains. Non classical buckling analysis involves considerations such as imperfections, non-elastic behaviour of the material, dynamic effects of the loading, the fact that the in-plane loading is not in the initial point of the plate.
Finally, it may point out that no plate is initially perfect (perfectly flat or perfectly symmetry) and if initial deviation (from flatness or symmetry) exists, the behaviour of the plate will follow the path similar with curve 1-5. In this case, no clear buckling phenomenon may be identifying. The deviations of the plate from the flatness and symmetry are usually called imperfections (initial transversal imperfections, delaminations) as it will be treated in the following chapters.
The following cases (in numerical and experimental ways) are presented: compressive buckling, shear buckling, mixed compressive and shear buckling. The results (for linear and nonlinear model) are presented as variation of the buckling loads function of maximum transversal displacement (buckling and post-buckling behaviour).
The state of equilibrium of a plate deformed by forces acting in the plane of the middle surface is unique and the equilibrium is stable if the forces are sufficiently small. If, while maintaining the distribution of forces constant at the edge of the plate, the forces are increased in magnitude, there may arise a time when the basic form of equilibrium ceases to be unique and stable and other forms become possible, which are characterized by the curvatures of the middle surface.
The equation of the deflected surface of symmetrically laminated plates is
 |
|
For symmetrically laminated cross-ply plates there is no coupling between bending and twisting. So, D16=D26=0. In this case, the equation (AA1) will have the form as the buckling equation for a homogeneous, orthotropic plate
where Dn, D22, D66, Di6, D26 are the orthotropic plate stiffnesses, calculated according to the equation
I N
![]() D = 3 L Q (3 – *3-1)
D = 3 L Q (3 – *3-1)
3 3=i
The thickness and position of every ply can be calculated from the equation
(AA4)
and
![]() (AA5)
(AA5)
The second and fourth terms from equation (AA2) are the measure of the orthotropic
coupling, resulting from the fact that the principal orthotropic axes are not orthogonal with the plate geometry axes.
Linear buckling of beams, membranes and plates has since been studied extensively. A linearized stability analysis is convenient from a mathematical viewpoint but quite restrictive in practical applications. What is needed is a capability for determining the nonlinear load-deflection behaviour of a structure. Considerable effort has also been expended on this problem and two approaches have evolved: class-I methods, which are incremental in nature and do not necessarily satisfy equilibrium; and class-II methods, which are self-correcting and tend to stay on the true equilibrium path (Thurley & Marshal, 1995).
Historically, class-I was the first finite element approach to solving geometrically non-linear problems (Ambarcumyan, 1991). In this method the load is applied as a sequence of sufficiently small increments so that the structure can be assumed to respond linearly during each increment.
To solving of geometrically and material nonlinear problems, the load is applied as a sequence of sufficiently small increments so that the structure can be assumed to respond linearly during each increment.
For each increment of load, increments of displacements and corresponding increments of stress and strain are computed. These incremental quantities are used to compute various corrective stiffness matrices (variously termed geometric, initial stress, and initial strain
matrices) which serve to take into account the deformed geometry of the structure. A subsequent increment of load is applied and the process is continued until the desired number of load increments has been applied. The net effect is to solve a sequence of linear problems wherein the stiffness properties are recomputed based on the current geometry prior to each load increment. The solution procedure takes the following mathematical form
(K + KI );1 Adj =AQ (AA6)
where
K is the linear stiffness matrix,
Ki is an incremental stiffness matrix based upon displacements at load step i-1,
Adi is the increment of displacement due to the i—th load increment,
AQ is the increment of load applied.
The correct form of the incremental stiffness matrix has been a point of some controversy. The incremental approach is quite popular (this is the procedure applied in all studies in this chapter). This is due to the ease with which the procedure may be applied and the almost guaranteed convergences if small enough load increments are used.
The plate material is damaged according to a specific criterion.
For various materials classes three dimensional failure criteria are developed. These include both isotropic and anisotropic material symmetries, and are applicable for macroscopic homogeneity. in the isotropic materials form, the properly calibrated failure criteria can distinguish ductile from brittle failure for specific stress states. Although most of the results are relevant to quasi-static failure, some are for time dependent failure conditions as well as for fatigue conditions.
The buckling load determination may use the Tsai-Wu failure criterion in the case if the general buckling does not occurred till the first-ply failure occurring. in this case, the buckling load is considered as the in-plane load corresponding to the first-ply failure occurring.
The Tsai-Wu failure criterion provides the mathematical relation for strength under combined stresses. Unlike the conventional isotropic materials where one constant will suffice for failure stress level and location, laminated composite materials require more elaborate methods to establish failure stresses. The strength of the laminated composite can be based on the strength of individual plies within the laminate. in addition, the failure of plies can be successive as the applied load increases. There may be a first ply failure followed by other ply failures until the last ply fails, denoting the ultimate failure of the laminate. Progressive failure description is therefore quite complex for laminated composite structures. A simpler approach for establishing failure consists of determining the structural integrity which depends on the definition of an allowable stress field. This stress field is usually characterized by a set of allowable stresses in the material principal directions.
The failure criterion is used to calculate a failure index (F. I.) from the computed stresses and user-supplied material strengths. A failure index of 1 denotes the onset of failure, and a value less than 1 denotes no failure. The failure indices are computed for all layers in each element of your model. During postprocessing, it is possible to plot failure indices of the mesh for any layer.
The Tsai-Wu failure criterion (also known as the Tsai-Wu tensor polynomial theory) is commonly used for orthotropic materials with unequal tensile and compressive strengths. The failure index according to this theory is computed using the following equation (Altenbach & all, 2004, Ambarcumyan, 1991).
F. I. – Fj • аг + F2 • о2 + Fu • Oj + F22 • о2 + F66 • о6 + 2F12 • ог • a2
![]()
where
The coefficient F12, which represents the parameter of interaction between a1 and a2, is to be obtained by a mechanical biaxial test. In the equations (AA8), the parameters R?, Rt are the compressive strength and tensile strength in the material in longitudinal direction (i=1) and transversal direction (i=2). The parameter R12 is in-plane shear strength in the material
1- 2 plane.
According to the Tsai-Wu failure criterion, the failure of a lamina occurs if
F. I. > 1. (AA9)
The failure index in calculated in each ply of each element. In the ply where failure index is greater than 1, the first-ply failure occurs, according to the Tsai-Wu criterion. In the next steps, the tensile and compressive properties of this element are reduced by the failure index. If the buckling did not appeared until the moment of the first-ply failure occurring, the in-plane load corresponding to this moment is considered as the buckling load.