 |
 |
 |
Independently of the discrete cellular automata, Dan Cohen, a botanist, implemented the first procedural method for the modeling of branching structures [29]. For each branching pattern a Fortran program was written using a set of simple growth rules.
Although here for each structure a new algorithm is programmed (we are dealing with a typical procedural approach), three relatively simple rules determine the growth and the type of branching in a structure:
■ Growth takes place only at the tips of the branches, i. e., the biological mechanism of the shoot is directly replicated.
■ The strengths and angles of the growth are determined by the current direction, a local density field, its gradient, and the resistance of the structure to changes of the angle.
■ The branching tendency is determined by a probabilistic measure that depends, aside from a general value, on the distance to the last branching and on the local density field.
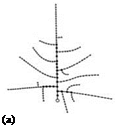
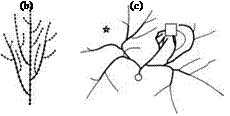
The model is developed through a sequence of discrete steps that are aligned according to the above set of rules. In Fig. 4.2, three branching structures can be seen, which were produced by application of varying rules. The effect of branching restrictions is shown in Fig. 4.2a. Part (b) demonstrates the possibilities of spatial adjustment. Figure 4.2c illustrates the application of attractors and inhibitors.
This approach also includes the changes of the parametric values outside the branching structures. This actually allows the visual differentiation in the orders of the branching, and it is used in many of the later works. Although the approach is not a rule-based method, Cohen points out how powerful rule systems are, and how important this type of branching structure is in botany.



