Scale and proportion are dependent on physical and spatial relationships, although important distinctions need to be made between these terms. Scale is based on the size of one thing relative to another, such as the size of a sectional sofa in relation to the size of a room. The floor lamp in Figure 6.16 is based on a series of reference points taken from the vertical axis of a human body (Figure 6.17). The individual parts of the lamp reference various heights of the body, which were determined from the figure. The sketch explores proportional relationships between the floor lamp and the human form at a scale of 1-to-1.
|
|
|
|

|

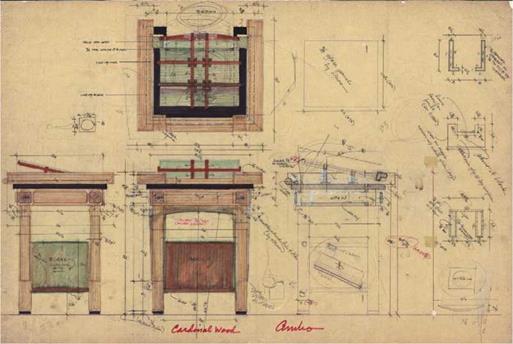
Proportion is the geometric correlations between parts and between parts and the whole. The design of the storage unit shown in Figure 6.18 is concerned primarily with proportional composition (formal geometric order) and secondarily with size or scale.
Scale
Furniture very often appears larger or smaller in its intended spatial context than it did in the shop where it was fabricated. The perception of scale depends on the size of the furniture and the spatial context in which it is placed. When the surrounding spatial environment changes, the relative perception of size will change as well, though the proportions of the furniture have not changed. Furniture draws relationships between objects and space, thereby giving scale to a room, but it also draws relationships to the human body, thereby indirectly giving scale to the room based on the body.
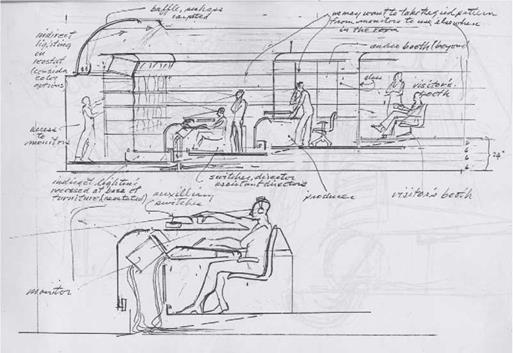
Parallel to the idea of relative size but different in focus is the scale in which designers sketch, draw, draft, or think about furniture. Initial conceptual ideas may be delineated at any scale. A plan of a space showing the furniture layout might be sketched, drafted, or plotted at У inch = 1 foot 0 inches or at 1/8 inch = 1 foot 0 inches. Interior elevations or sections showing furniture in elevation may be sketched, drawn, or plotted at У2 inch = 1 foot 0 inches scale (Figure 6.19). Detailed hard-line drawings or plotted working drawings at a scale of 3 inches = 1 foot 0 inches (25 percent of full size) is the conventional scale used to document the overall dimensions of individual pieces of furniture (Figure 6.20). It is helpful to show the edge profile, joinery, and mechanical features (as detailed section drawings) at full scale.
Placement and orientation are important aspects of furniture design. Because architects and interior designers incorporate furniture into the plans and sections of their drawings,
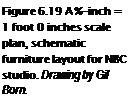 |
 |
designers should think about the context of furniture in the conception of design and be able to sketch, model, and develop furniture designs in a range of scales from 1/8 inch = 1 foot 0 inches to full scale.
Proportion
 |
 |
Proportion is not about size, nor is it about the perception of scale. It is the mathematical relationships of a part or parts of a design to other parts within a given field or frame of reference. We recognize furniture by its proportions, identifying the relationships between
seat pan to seat back and leg dimensions to table height dimensions. Proportion is the relationship between width and length and, concurrently, between height and depth. Furniture can appear visually heavy or light, compressed or extended. How we characterize the physical and spatial relationships of furniture reveals proportional relationships of the design.
Proportion is based on a variety of tangible relationships. The human body is the most common reference used in the design of furniture. Other proportional systems include mathematical or geometric systems such as the Golden Section, the Fibonacci series of numbers, the root system, fractal geometry, and logarithmic or parabolic geometry. The Power of Limits, written by Gyorgy Doczy, is a good resource for further reading on proportion.




